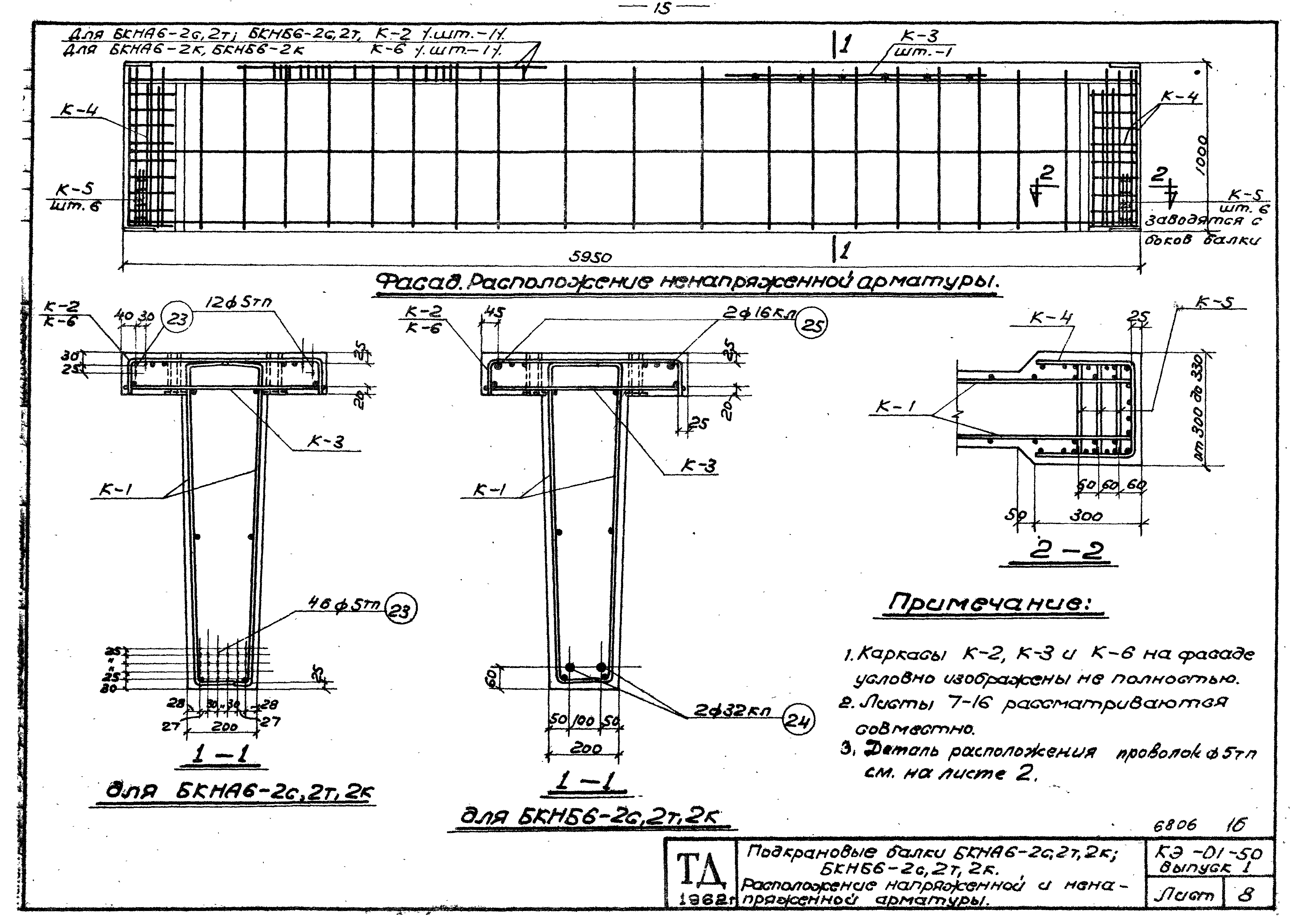
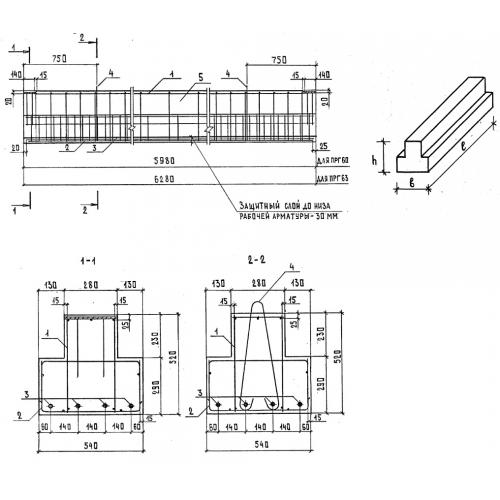
Балки таврового сечения железобетонные: Железобетонные балки сечения таврового и двутаврового
|
|
Расчет железобетонной балки таврового сечения
Теоретические основы расчетаСогласно СНиП 2. 03.01-84 и СП 52-101-2003 расчет тавровых поперечных сечений без арматуры в сжатой зоне рекомендуется выполнять с использованием следующих положений:
03.01-84 и СП 52-101-2003 расчет тавровых поперечных сечений без арматуры в сжатой зоне рекомендуется выполнять с использованием следующих положений:
1. а) Если нейтральная плоскость (граница между сжимаемой и растягиваемой зонами сечения) проходит в полке (рисунок 326.1.а), т.е. соблюдаются условия:
RsAs < Rbb’fh’f (326.1.1)
M ≤ Rbb’fh’f(ho — 0.5h’f) (326.1.2)
и
ξ = у/ho < ξR (220.6.1)
то расчет производится, как для балки прямоугольного сечения с шириной b’f. Подробности расчета по такому алгоритму подробно расписаны в статье «Расчет железобетонной плиты перекрытия«. Здесь же приведу только основные формулы:
ξR — предельно допустимое значение относительной высоты сжатой зоны бетона, определяемое по следующей формуле:
(220. 6.2)
6.2)
где Rs — расчетное сопротивление арматуры в МПа. Также предельное значение относительной высоты сжатой зоны бетона можно определить по таблице:
Таблица 220.1. Граничные значения относительной высоты сжатой зоны бетона
Примечание: При выполнении расчетов не профессиональными проектировщиками, ограничивающимися только расчетами по первой группе предельных состояний, я рекомендую занижать предельное значение относительной высоты сжатой зоны
При определении сечения арматуры сначала определяется коэффициент am:
(220.6.6)
при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.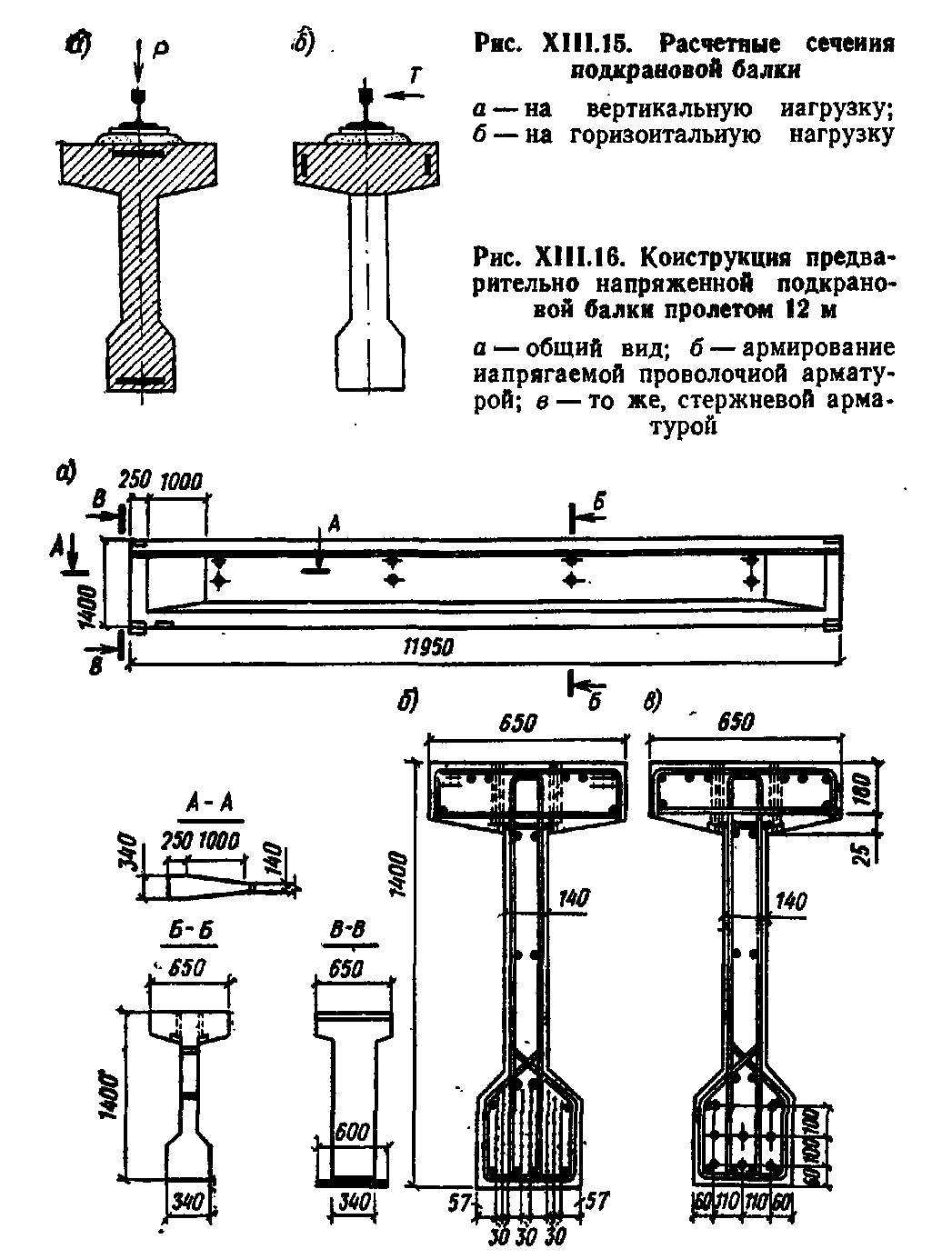 1.
1.
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
(220.6.7)
В формулах (220.6.6) и (220.6.7) значения b заменяются на b’f.
Рисунок 326.1
1. б) Если нейтральная плоскость проходит в ребре балки (рисунок 326.1.б), то расчет выполняется, исходя из следующего условия:
M < Rbbу (h0 — 0,5у) + Rbh’f(b’f — b)(h0 — 0.5h’f) (326.2)
где (b’f — b)h’f = Aov — площадь сечения свесов полки.
При этом высота сжатой зоны у определяется, исходя из следующих формул:
RsAs = Rbby + Rbh’f(b’f — b) (326.3.1)
y = (RsAs — RbAov)/Rbb (326.3.2)
при этом высота сжатой зоны принимается у ≤ ξRho.
При определении сечения арматуры сначала определяется коэффициент am:
(326.4.1)
при аm < aR арматура в сжатой зоне не требуется, значение
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
(326.4.2)
2.Так как ширина полки таврового сечения может быть достаточно большой, например для балок, входящих в состав балочного монолитного перекрытия, то ширина полки балки b’f принимается с учетом следующих условий:
2.1. Ширина свеса полки в каждую сторону от ребра балки bсв = (b’f — b)/2 (на рисунке 326 не показана) должна быть не более 1/6 длины пролета рассчитываемого элемента, а также не более:
2.2. При наличии поперечных ребер (второстепенных балок при расчете главных балок или главных балок при расчете второстепенных балок, при этом ребро рассматриваемой балки считается продольным) или при 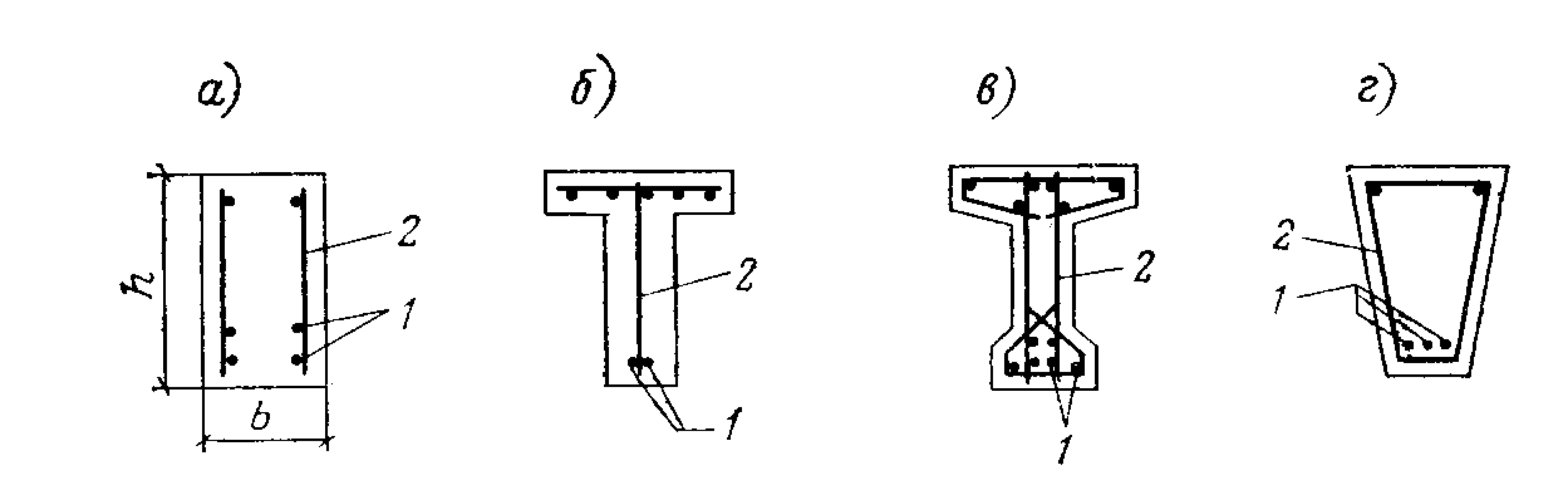 1h расчетная ширина полки b’f принимается равной 1/2 расстояния между продольными ребрами в свету.
1h расчетная ширина полки b’f принимается равной 1/2 расстояния между продольными ребрами в свету.
2.3. При отсутствии поперечных ребер или при расстоянии между поперечными ребрами большем, чем расстояния между продольными ребрами и при h’f < 0.1h расчетная ширина полки b’f = 6h’f.
2.4. При консольных свесах полки (при расчете отдельных балок таврового сечения, не входящих в состав разного рода перекрытий):
а) при h’f ≥ 0.1h расчетная ширина полки b’f = 6h’f;
б) при 0.05h ≤ h’f < 0.1h расчетная ширина полки b’f = 3h’f;
в) при h’f < 0.05h свесы полок в расчетах не учитываются.
2.5. При изменяющейся высоте свесов полки в расчетах допускается использовать среднее значение высоты h’f.
Все это, так сказать, теоретические, а потому не совсем понятные положения, давайте посмотрим, как их можно применить на практике.
Пример расчета на прочность балки таврового сечения
Планируется монолитное перекрытие в жилом помещении размерами 5х8 метров с 4 главными балками. Предварительно принятая высота основной плиты 8 см, предварительные размеры балок 10х15 см:
Рисунок 326.2
Примечание: На общей расчетной схеме (рис.326.2.а) размеры даны в миллиметрах, а размеры поперечного сечения балки (рис.326.2.б) даны в сантиметрах для упрощения дальнейших расчетов. Конструктивная арматура основной плиты для упрощения расчетов не учитывается.
1. Если и основная плита и балки будут бетонироваться одновременно, то высота основной плиты будет высотой полки h’f, а общая высота тавровой балки h = 8 + 15 = 23 см, а = 2.5 см, ho = 20.5 см. Для перекрытия будет использоваться бетон класса В20, с расчетным сопротивлением сжатию Rb = 11.5 МПа (117 кгс/см2) и арматура класса AIII (А400), имеющая расчетное сопротивление растяжению Rs = 355 МПа (3600 кгс/см2).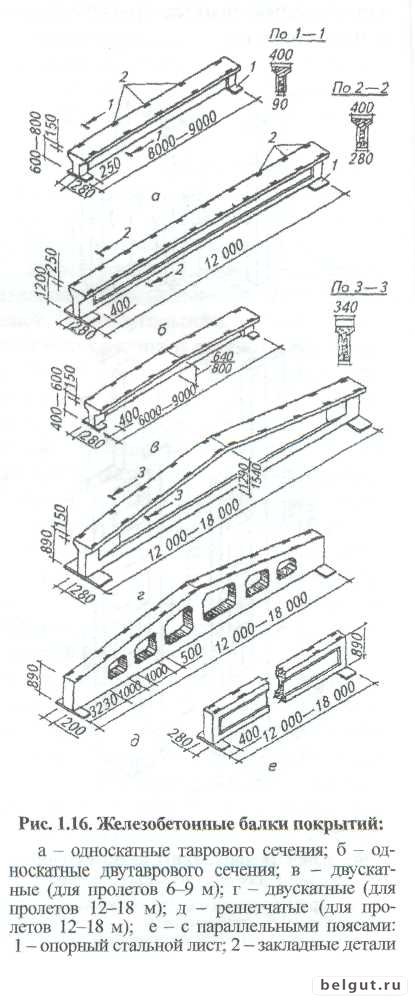 В случае если бетонная смесь будет приготавливаться в домашних условиях (т.е. без должного контроля прочности образцов) и бетонирование будет выполняться не специалистами расчетное сопротивление бетона следует понизить. СНиПом СНиП 2.03.01-84 понижающий коэффициент, учитывающий качество выполнения работ, для подобных случаев не предусмотрен, да и тяжело предугадать, насколько сильно вышеуказанные причины могут повлиять на расчетное сопротивление бетона. Ориентировочно значение этого коэффициента может составлять от 0.5, если нет уверенности в своих силах, до 0.9, если уверенность в своих силах высокая. Дальнейший расчет будет производиться с использованием коэффициента качества работ γк = 0.9. Тогда расчетное значение сопротивления бетона сжатию составит:
В случае если бетонная смесь будет приготавливаться в домашних условиях (т.е. без должного контроля прочности образцов) и бетонирование будет выполняться не специалистами расчетное сопротивление бетона следует понизить. СНиПом СНиП 2.03.01-84 понижающий коэффициент, учитывающий качество выполнения работ, для подобных случаев не предусмотрен, да и тяжело предугадать, насколько сильно вышеуказанные причины могут повлиять на расчетное сопротивление бетона. Ориентировочно значение этого коэффициента может составлять от 0.5, если нет уверенности в своих силах, до 0.9, если уверенность в своих силах высокая. Дальнейший расчет будет производиться с использованием коэффициента качества работ γк = 0.9. Тогда расчетное значение сопротивления бетона сжатию составит:
Rb = 117·0.9 = 105.3 кг/см2
2. Пролет балок составляет 5 м, при этом bсв ≤ 500/6 = 83 см, первое условие соблюдается. Рассматриваемая балка входит в состав монолитного перекрытия, при этом высота плиты 8 см > 0.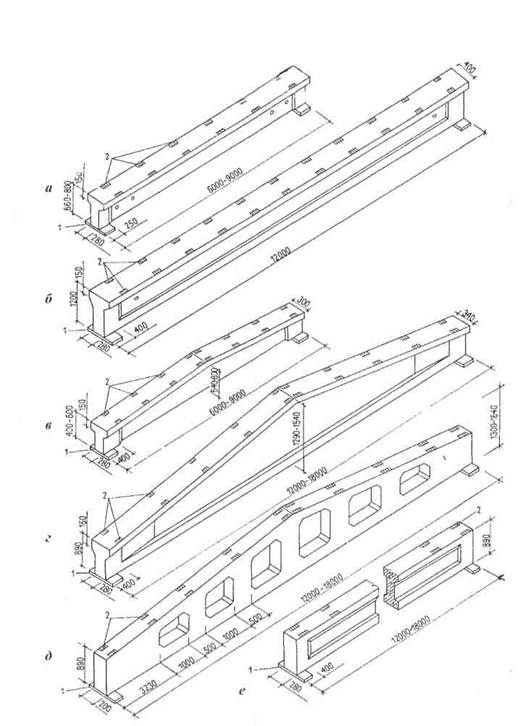 1h = 2.3 см, согласно п.2.2 расчетная ширина полки составит:
1h = 2.3 см, согласно п.2.2 расчетная ширина полки составит:
b’f = 152/2 = 76 см
3. Для определения высоты сжатой зоны сечения сначала необходимо определить максимальный изгибающий момент, действующий в рассматриваемом поперечном сечении тавровой балки. А для этого нужно знать нагрузки, действующие на перекрытие.
При расчете перекрытий жилых зданий в качестве расчетной временной нагрузки можно использовать следующее значение qвр = 400 кг/м2. Для балок с шагом 162 см расчетная временная нагрузка на погонный метр составит
qвр = 400·1.62 = 648 кг/м
Примечание: Более точное значение расчетной нагрузки следует определять по СНиП 2.01.07-85 «Нагрузки и воздействия», где приводятся значения нормативных нагрузок. Согласно указанного СНиП для плит перекрытий в квартирах жилых зданий нормативное значение распределенной нагрузки составляет 150 кг/м2. Затем это значение нужно умножить на коэффициент надежности по нагрузке, при таком значении нормативной нагрузки составляющий γн = 1.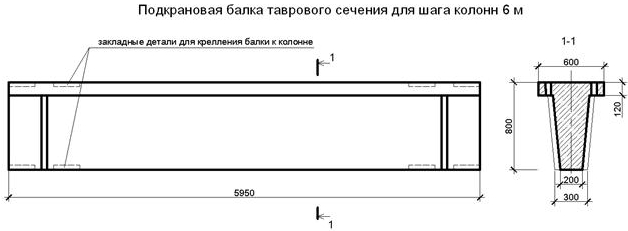 3 (1.4 по старым нормам). Таким образом расчетное значение временной нагрузки без учета стяжки, напольного покрытия и возможных других временных нагрузок составит
3 (1.4 по старым нормам). Таким образом расчетное значение временной нагрузки без учета стяжки, напольного покрытия и возможных других временных нагрузок составит
qсв = 150·1.3 = 195 кг/м2
Как показывает практика, если к определенной таким образом временной распределенной нагрузке прибавить временные нагрузки от выравнивающей стяжки, напольного покрытия и др., умноженные на соответствующие коэффициенты надежности по нагрузке, то суммарная временная нагрузка будет немного меньше указанных 400 кг/м2. Если до начала расчетов известна толщина будущей стяжки, вид напольного покрытия, расположение мебели и инженерного оборудования, то значение суммарной временной нагрузки можно рассчитать более точно. При этом значение расчетной временной нагрузки может снизиться на 30-70 кг/м2. Тем не менее дальнейший расчет будет выполняться по указанной выше временной нагрузке 400 кг/м2.
Примечание: Устройство каких-либо перегородок данным расчетом не предусматривается.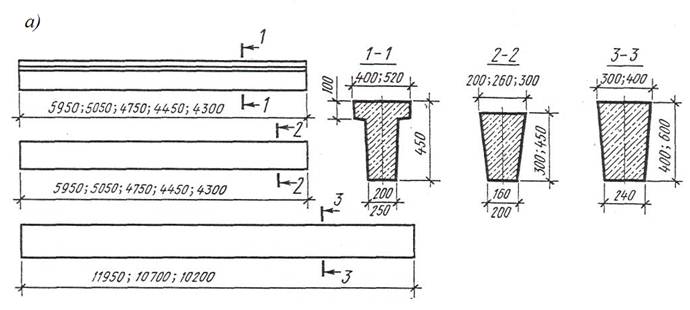 Если по перекрытию планируется устройство перегородок, то следует предусмотреть отдельные балки под перегородки и рассчитать их с учетом возможных нагрузок. Исключение могут составлять легкие перегородки из ГКЛ, возле которых не будет устанавливаться мебель.
Если по перекрытию планируется устройство перегородок, то следует предусмотреть отдельные балки под перегородки и рассчитать их с учетом возможных нагрузок. Исключение могут составлять легкие перегородки из ГКЛ, возле которых не будет устанавливаться мебель.
Постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.08·1.62 + 0.1·0.15)2500 = 361.5 кг/м. Коэффициент надежности по нагрузке для бетонных и железобетонных конструкций составляет γн = 1.1. Тогда расчетное значение постоянной нагрузки составит qпр = 361.5·1.1 = 397.65 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 397.65 +648 = 1045.65 кг/м
Тогда максимальный изгибающий момент для бесконсольной балки на двух шарнирных опорах:
Мmax = ql2/8 = 1045.65·52/8 = 3267.656 кг·м = 326765.6 кг·см
Почему это так, достаточно подробно рассказывается в другой статье.
4. Проверяем выполнение условия (326.1.2):
M = 326765.6 < Rbb’fh’f(ho — 0.5h’f) = 105.3·76·8(20.5 — 4) = 1056369.6
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 326765.6/(105.3·76·20.52) = 0.09716
6. am = 0.09716 < aR = 0.39/1.5 = 0.26, значит арматура в сжатой зоне не требуется, тогда требуемая площадь сечения арматуры в растянутой зоне составит:
Аs = 105.3·76·20.5(1 — √1 — 2·0.09716)/3600 = 4.67 см2
Диаметр арматуры можно подобрать по следующей таблице:
Таблица 2. Площади поперечных сечений и масса арматурных стержней.
7. Для армирования балки можно использовать 2 стержня диаметром 18 мм, площадь сечения стержней составит 5.09 см2.
8. Проверяем соблюдение необходимой толщины защитного слоя бетона при выбранной арматуре. Толщина защитного слоя согласно п.5.5 СНиП 2.03.01-84 должна быть не менее диаметра арматуры и ≥ 15 мм. В нашем случае толщина защитного слоя бетона составит:
Толщина защитного слоя согласно п.5.5 СНиП 2.03.01-84 должна быть не менее диаметра арматуры и ≥ 15 мм. В нашем случае толщина защитного слоя бетона составит:
hз = а — d/2 = 25 — 18/2 = 16 мм
Условие не выполнено, поэтому для расчетов следует принять большее значение а. Например, при а = 27 мм ho = 20.3 см.
аm = 326765.6/(105.3·76·20.32) = 0.0991
Аs = 105.3·76·20.3(1 — √1 — 2·0.0991)/3600 = 4.71 см2
9. Расстояние в свету между стержнями арматуры составит 100 — 2а — d = 100 — 54 — 18 = 28 мм. Это означает, что для для бетонирования балки следует использовать бетонную смесь с максимальным размером зерен щебня 28 мм. Если предполагается использование крупного заполнителя больших размеров, то следует или увеличить ширину балки, или увеличить высоту балки, что позволит уменьшить диаметр используемой арматуры.
Примечание: если балки и плита будут бетонироваться отдельно, то тогда балки следует рассчитывать как элементы прямоугольного сечения с высотой, равной высоте балок.
Пример расчета балки таврового сечения с учетом прогиба
Выполненный выше расчет на прочность (расчет по первой группе предельных состояний) как правило для шарнирно опертых однопролетных балок недостаточен и требует дополнительного расчета по деформациям. Методик определения прогиба ж/б конструкций существует несколько. На мой взгляд проще всего определить приблизительное значение прогиба при расчете по допускаемым нагрузкам.
Расчет по допускаемым нагрузкам, предполагающий упругую работу материала и не предусматривающий пластические деформации в сжатой зоне бетона, дает следующие результаты:
При определенных выше параметрах высота сжатой зоны бетона составит:
y = √3M/2b’fRb = √3·326765.6/2·76·105.3 = 7.826 см
При этом требуемая высота сжатой зоны при расчете по деформациям определяется решением следующего кубического уравнения:
у3 = 3As(ho — y)2Es/b’fEb (321. 2.4)
2.4)
и при Еb = 270000 кгс/см2, Es = 2000000 кгс/см2, составит примерно уf = 6.53 см (ур = 5.234 см).
Тогда при Ip = b’f(2yp)3/12 = 76(2·5.234)3/12 = 7264.8 см4 примерный прогиб балки составит:
f = 0.83·5·10.456·5004/(384·270000·7264.8) = 3.6 см > fu = 500/250 = 2 см (согласно СНиП 2.01.07-85)
Это достаточно большой прогиб и для его уменьшения можно увеличить количество балок, но можно и увеличить высоту и ширину сечения принятого количества балок, тем более, если это необходимо сделать для использования бетонной смеси с крупным щебнем. Например, при увеличении высоты балки всего на 2 см — до 17 см и ширины балки до 11 см и при той же арматуре ho = 22.3 см:
уf = 7 см (yp = 6.174 см), Ip = 76(2·6.174)3/12 = 11924 см4, приблизительный прогиб
f = 0. 83·5·10.456·5004/(384·270000·11924) = 2.194 см ≈ fu = 2 см.
83·5·10.456·5004/(384·270000·11924) = 2.194 см ≈ fu = 2 см.
Примечание: приведенная методика определения прогиба не является рекомендованной нормативными документами, к тому же для упрощения расчетов не учитывалось то, что немного увеличится нагрузка от собственного веса балки. Тем не менее такая методика позволяет достаточно быстро определить приблизительное значение прогиба и оценить его влияние на работу конструкции.
Пример расчета на прочность балки таврового сечения с учетом изменения высоты полки
Так как при расчетах плиты принята новая высота плиты h = 6 см, то это вносит ощутимые изменения в значение постоянной нагрузки и в параметры тавровой балки.
В этом случае при общей высоте балки h = 25 см постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.06·1.62 + 0.11·0.19)2500 = 295.25 кг/м. Тогда расчетное значение постоянной нагрузки составит qпр = 295. 25·1.1 = 324.8 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
25·1.1 = 324.8 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 324.8 +648 = 972.8 кг/м
Мmax = ql2/8 = 972.8·52/8 = 3040 кг·м = 304000 кг·см
4. Проверяем выполнение условия (326.1.2):
M = 304000 < Rbb’fh’f(ho — 0.5h’f) = 105.3·76·6(22.3 — 3) = 926724.2
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 304000/(105.3·76·22.32) = 0.07638
Аs = 105.3·76·22.3(1 — √1 — 2·0.07638)/3600 = 3.943 см2
Как видим требуемая площадь сечения уменьшилась, но так как мы принимали сечение арматуры с учетом прогибов, то диаметр арматуры оставляем без изменения 2 стержня d = 18 мм.
При этом высота сжатой зоны бетона составит:
y = √3M/2b’fRb = √3·304000/2·76·105.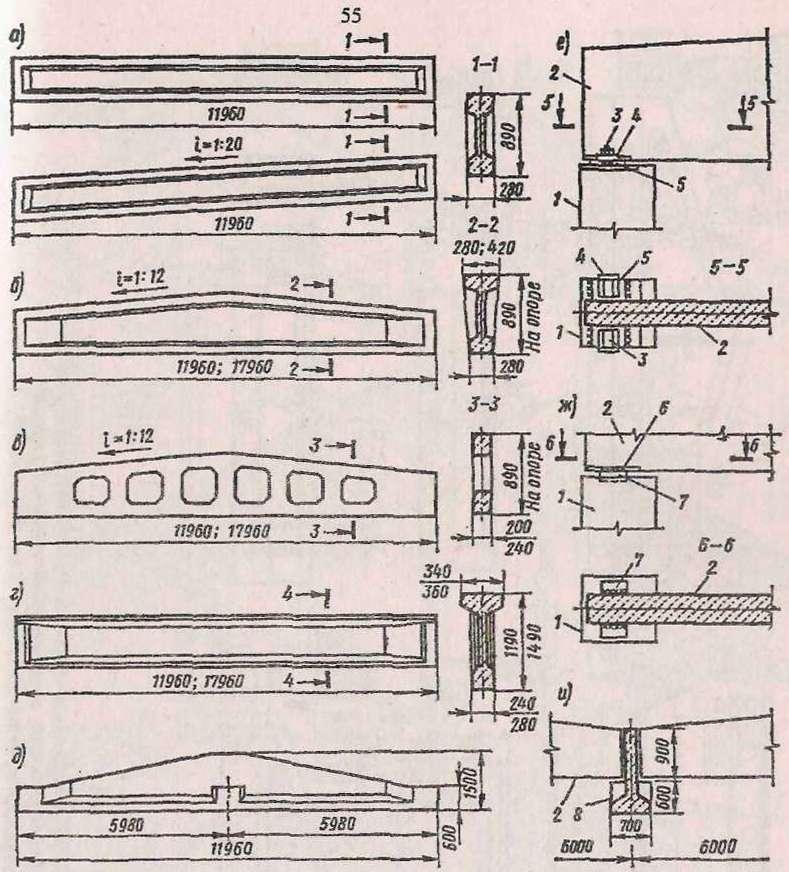 3 = 7.55 см
3 = 7.55 см
Требуемая высота сжатой зоны при расчете по деформациям составит примерно уf = 7.07 см
Однако такая высота сжатой зоны означает, что нейтральная линия будет проходить не в полке а в ребре балки, и значение утакже будет другим.
По более точной формуле значение моментов инерции полусечений составит:
Iв = b’fhf(y/2)2 +b’fhf3/12 + b(y — hf)((y — hf)/2)2 + b(y — hf)3/12 = Iн = As(ho — y)2Es/Eb (321.2.3.2)
тогда, подставив имеющиеся значения, получим:
76·6(у/2)2 + 76·63/12 + 11(у — 6)(y/2 — 3)2 + 11(y — 6)3/12 = 5.09(22.3 — y)22000000/270000;
114y2 + 1368 + 2.75(y — 6)3 + 0.917(y — 6)3 = 43.704(22.3 — y)2;
у ≈ 8. 08 см
08 см
Так как требуемая высота сжатой зоны при расчете на прочность больше, чем высота сжатой зоны при расчете по деформациям (разница составит примерно 7.55-7.05 = 0.5 см), то при приближенном расчете (без учета области пластических деформаций) расчетное значение высоты полки составит 6 — 0.5 = 5.5 см, тогда
Ip = 76·5.5·3.792 + 76·5.53/12 + 3.667·2.083 = 6004.2 + 1053.71 +33 = 7090.9 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 3.43 см > fu = 2 см, а значит высоту балок желательно увеличить еще.
Например, при общей высоте h = 30 см
у ≈ 10.02 см
Ip = 76·5.5·4.762 + 76·5.53/12 + 3.667·4.023 = 9470.9 + 1053.71 + 238.2 = 10762.8 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 1.9 см < fu = 2 см
Если произвести расчет с учетом изменяющего модуля упругости бетона, то при Еb1 = 270000/(1 + 2. 8) = 71052.6 кг/см2.
8) = 71052.6 кг/см2.
76·6(у/2)2 + 76·63/12 + 11(у — 6)(y/2 — 3)2 + 11(y — 6)3/12 = 5.09(27.3 — y)22000000/71052.6;
114y2 + 1368 + 2.75(y — 6)3 + 0.917(y — 6)3 = 166.0752(27.3 — y)2;
у ≈ 14.45 см и в этом случае высота сжатой области сечения принимается без изменений, тогда
Ip = 2·27410 = 54820 см4, тогда примерный прогиб балки составит:
f = 0.96·5·9.73·5004/(384·71052.6·54820) = 1.95 см < fu = 2 см
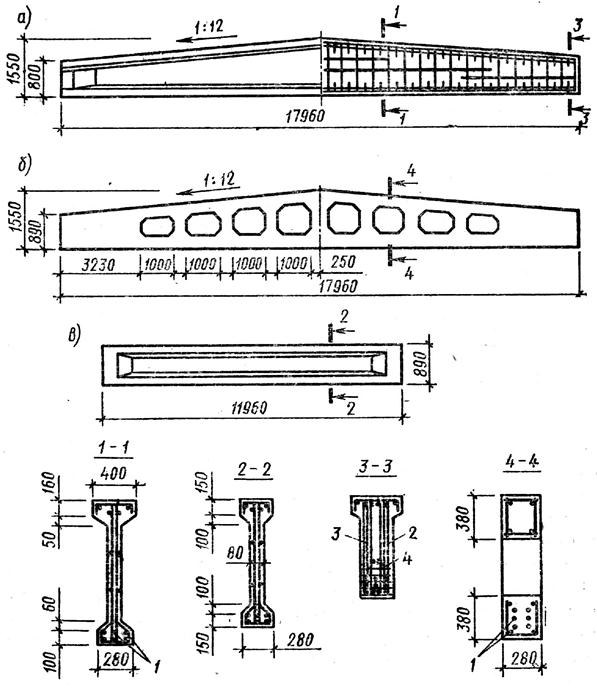
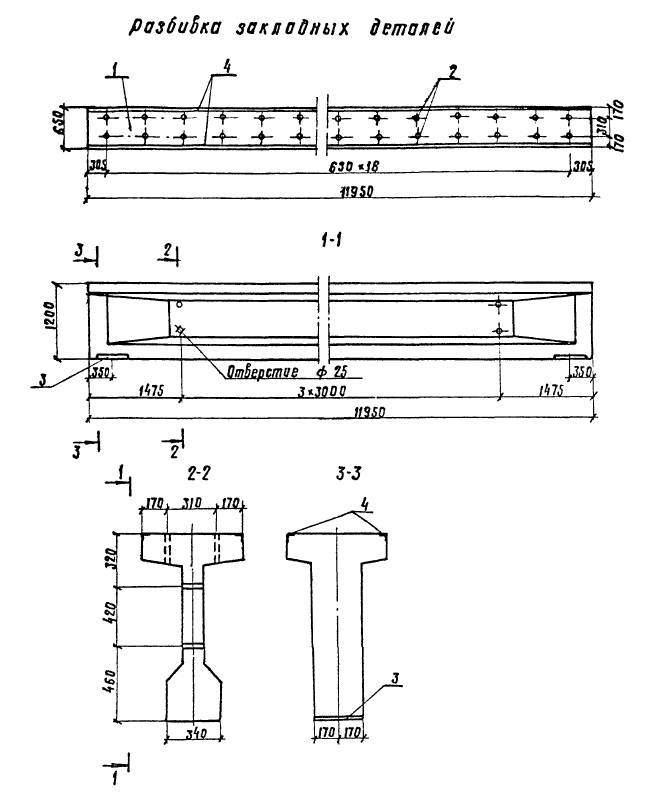
ПК-01-05 выпуск 2 «Железобетонные сборные несущие конструкции для покрытий с рулонной кровлей. Усиление балок пролетом 12 и 15м»
ПК-01-05 выпуск 2 «Железобетонные сборные несущие конструкции для покрытий с рулонной кровлей. Усиление балок пролетом 12 и 15м»1. В выпуске 2 серии ПК-01-05 дана конструкция усиления балок пролетом 12 и 15м, разработанных в выпуске 1 серии ПК-01-05, изготовленных и установленных в покрытия, как в строящихся, так и в эксплуатируемых зданиях.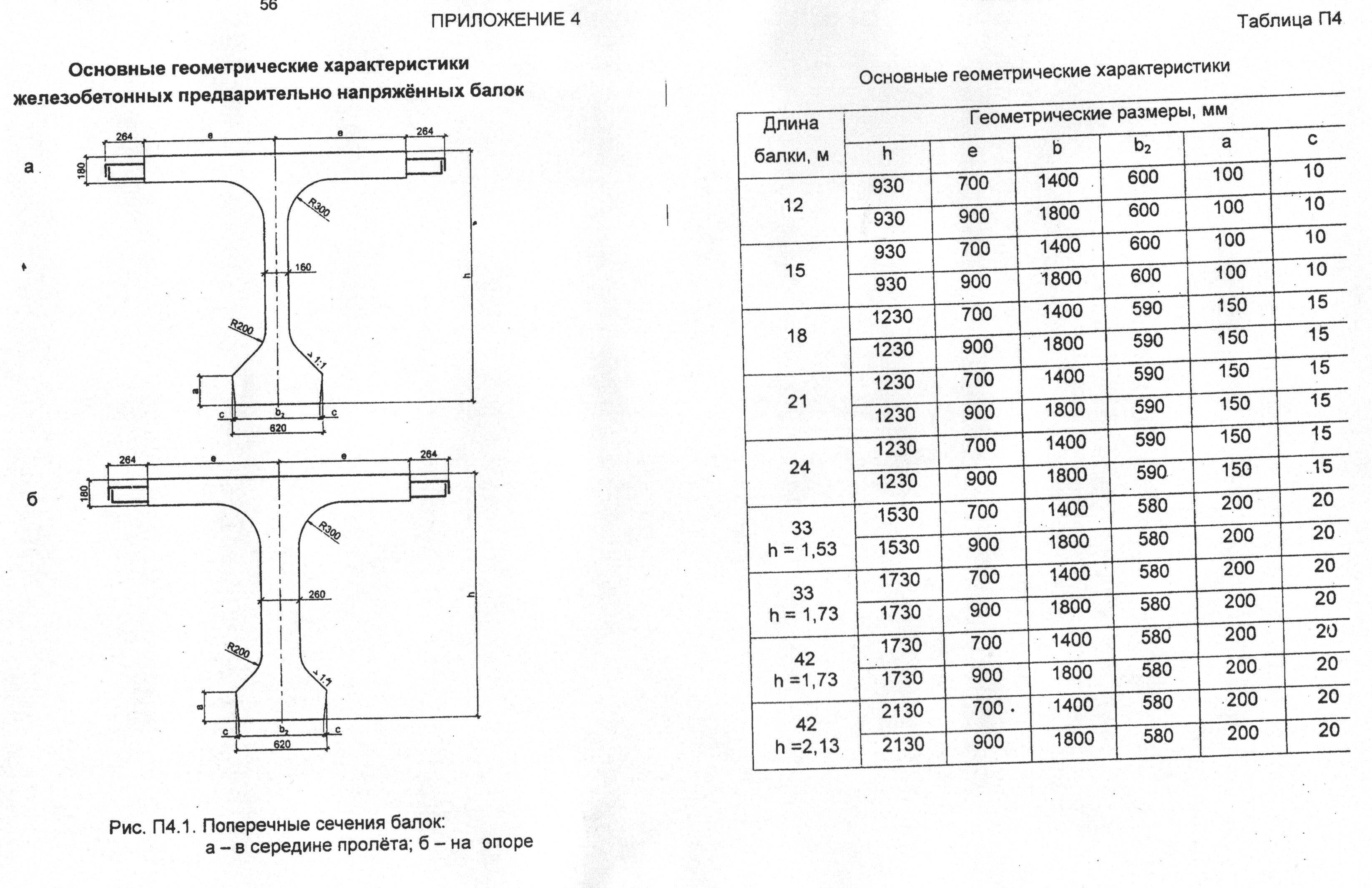
Усилению подлежат балки, отобранные в результате осмотра, согласно консультации, опубликованной в «Бюллетене строительной техники» №10 за 1961 год и приложенной к данному выпуску.
2. Настоящие чертежи усиления балок не предусматривают отклонений от типовых чертежей серии ПК-01-05 в части опалубочных размеров, марки бетона, расположения закладных частей, сколов бетона и т.д. При наличии отклонений конструкция и детали усиления должны решаться в индивидуальном порядке.
3. Конструкция усиления принята в виде шпренгеля на условия восприятия им 45-50% расчетной нагрузки, действующей на балку.
4. Арматура шпренгеля принята из стали марок 25Г2С или 35ГС.
5. Расчетное сопротивление арматуры при расчете на прочность принято 0,8*3400=2720кг/см2.
6. Расчетное сопротивление бетона торца балки при расчете на местное смятие принято 125кг/см2 для бетона марки 200 и 200кг/см2 для бетона марки 300.
7. Предварительное напряжение шпренгеля производится в зависимости от действующей на балку нагрузки в момент усиления.
8. Основным вариантом шпренгеля является вариант с гайками у опор балок. Натяжение при этом производится путем нагрева стержня электротоком или другим способом.
9. Контроль натяжения производится по удлинению шпренгеля.
10. Коротыши с резьбой привариваются к основному стержню стыковой сваркой или ванной сваркой на медной подкладке.
11. Усиление шпренгелем может быть осуществлено также с регулировкой удлинения шпренгеля при помощи муфт, расположенных по середине балки, при этом стержни шпренгеля ввариваются в боковые пластины.
12. Порядок производства работ в основном варианте принят следующим:
- верхняя полка у опор балок скалывается, как указано на чертежах;
- в зазоры между торцами балок (двух смежных пролетов и в торцах балок крайних пролетов) устанавливаются на растворе марки 300 стальные пластины, а зазоры между пластинами и торцами балок заполняются цементным раствором путем инъекцирования или забивки раствора в щели (в этом случае пластины устанавливаются насухо между торцами балок).
 Кроме того зазор между балками можно предварительно заполнить цементным раствором и забить в него пластину, для чего одна грань последней скошена.
Кроме того зазор между балками можно предварительно заполнить цементным раствором и забить в него пластину, для чего одна грань последней скошена. - к пластинам привариваются
- вставляется стержень и производится его предварительная подтяжка с помощью гаек, при этом провисание горизонтального участка шпренгеля должно быть ликвидировано проволочными подвесками, закрепленными к балке;
- нарезанные конца коротышей, выступающие из гаек, закрашиваются;
- производится нагревание стержней и подтягивание гаек одновременно в четырех местах, при этом сумма длин незакрашенных участков резьбы одного стержня должны соответствовать расчетному удлинению. Возможно поочередное подтягивание двух гаек у каждого торца. Запрещается подтягивание гаек на одной боковой стороне балки.
- величина незакрашенного участка резьбы фиксируется актом.
13. Производство работ по дополнительному варианту отличается только тем, что подтягивание производится муфтами (вместо гаек).
14. Организация, производящая работы по усилению балок с применением электронагрева должна разработать мероприятия техники безопасности по защите рабочих от действия электрического тока.
15. После окончания натяжения металлоконструкции окрасить.
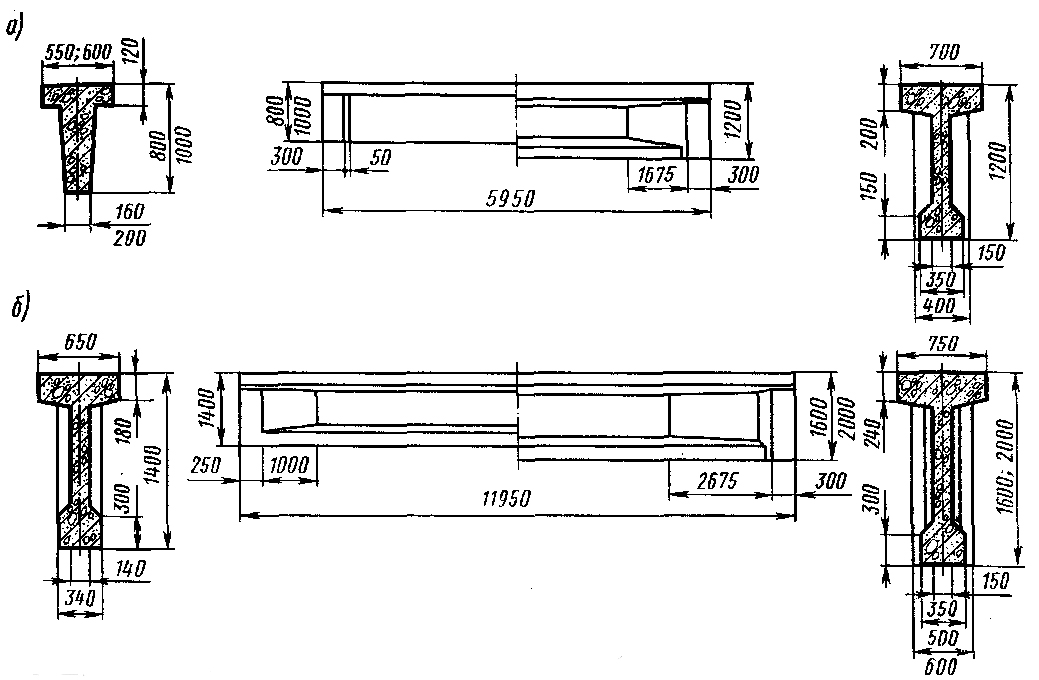
Консультация о применении в строительстве типовых сборных железобетонных ненапряженных балокСборные железобетонные ненапряженные балки таврового сечения с плоским сварным каркасом без отгибов начали применяться в 1953г. До 1955г. они входили в состав типовых чертежей серии ПК-01-03 выпуск 2, выпущенных на основе проектного предложения института Промстройпроект, а позднее вошли в состав серии ПК-01-05 выпуск 1.
Госстрой СССР приказом №299 от 24.11.1955г. срок применения рабочих чертежей серии ПК-01-05 ограничил 1957 годом, а в декабре 1959 года Госстрой СССР приказом№505 запретил применение балок пролетом 12 и 15м, как менее эффективных по сравнению с предварительно напряженными железобетонными балками.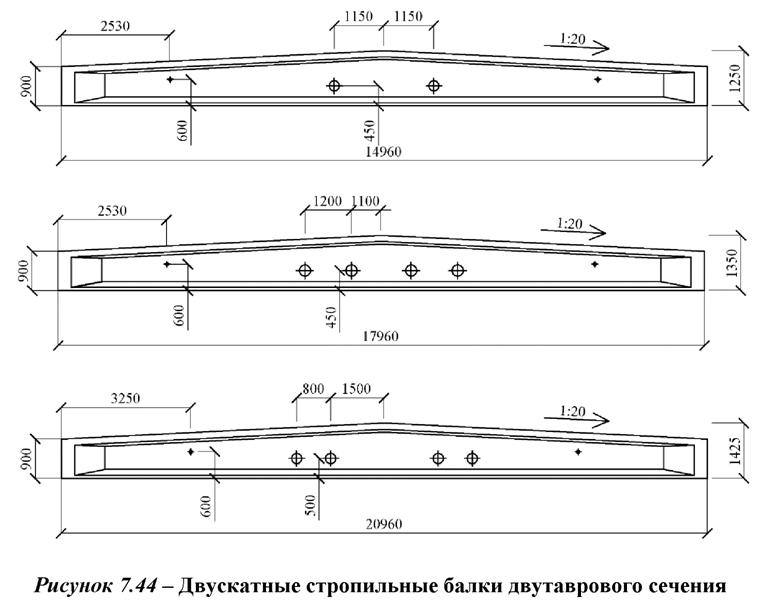
За истекшие годы балки применялись на многих объектах, они показали свою надежность. имевшие место единичные случаи разрушения смонтированных балок происходили, главным образом, по причине отступления от проекта или некачественного изготовления (низкие марки бетона, плохая анкеровка арматуры, отсутствие приварки анкерных уголков и т.п.)
В 1960-1961г.г. произошло несколько случаев обрушения этих балок в недостроенных цехах при очень низких температурах наружного воздуха (от -30 до -45С). Обрушения произошли из-зи хрупкого разрыва пакета арматуры в месте стыка нижнего стержня с односторонней накладкой поверх пакета.
Скачать ПК-01-05 выпуск 2 «Железобетонные сборные несущие конструкции для покрытий с рулонной кровлей. Усиление балок пролетом 12 и 15м»
Железобетонная балка таврового сечения для строительства мостов
При строительстве мостов и различных путепроводов используется такое прочное изделие, как железобетонная балка таврового сечения.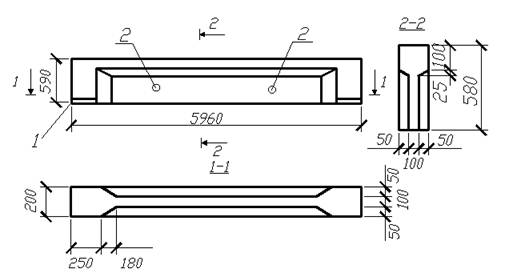 Она обладает такими достоинствами, как:
Она обладает такими достоинствами, как:
- морозостойкость;
- стойкость к трещинам;
- стойкость даже к сильным нагрузкам;
- подходит для интенсивной эксплуатации;
- железобетонное изделие выдерживает большой вес.
Построенные с использованием двутавровых балок автомобильные виадуки и мосты будут отвечать всем требованиям безопасности. Ведь они будут надежными, прочными. Так как железобетонная балка таврового сечения рассчитана на многолетний срок использования, то и мосты простоят не одно десятилетие, сохраняя свои прочностные качества.
Для выпуска балок используется бетон и арматура. Металлическая арматура используется для усиления создаваемой конструкции. Она создает каркас, который предохраняет бетон от разрушения и растрескивания. Бетон при выпуске изделий используется тяжелый. Арматура может быть выполнена из следующих видов стали – Ст3, 35ГС и других. Арматура, которая устанавливается в изделие, может быть как напрягаемой, так и ненапрягаемой. Ее выбор будет обусловлен для производителя конкретным видом балки, которую он будет изготавливать, и предписанным для нее ГОСТом.
Ее выбор будет обусловлен для производителя конкретным видом балки, которую он будет изготавливать, и предписанным для нее ГОСТом.
При покупке балок надо выбирать изделия, которые будут соответствовать нормам. Все железобетонные изделия перед строительством путепроводов будут проверяться специальной комиссией по строительству мостов. Если в балках будут выявлены дефекты, то их комиссия не примет. Поэтому при покупке таких железобетонных изделий требуется найти продавца, у которого можно гарантированно приобрести качественные ЖБИ. И этим поставщиком может стать компания «Стройбург», которая может предложить как разные виды двутавровых балок, так и различные типы другой продукции из железобетона.
Железобетонные конструкции. II часть. Бушков В.А. 1941 | Библиотека: книги по архитектуре и строительству
Предисловие
Раздел I. Изгиб и скалывание при изгибе
Глава I. Конструкции, работающие на изгиб и скалывание при изгибе. Плоские покрытия и перекрытия
Плоские покрытия и перекрытия
Глава II. Статический расчет изгибаемых элементов железобетонных конструкций
1. Предварительные сведения
2. Расчет балочных плит
3. Расчет плит, опертых по контуру (плиты с перекрестной арматурой)
4. Расчет балок
Глава III. Работа балки на изгиб. Три стадии напряженности
Глава IV. Расчет прочности балок на изгиб
A. Прямоугольная балка или плита с одиночной арматурой
1. Формулы для определения Mp и плеча пары внутренних сил z
2. Опытная проверка расчетной формулы Mp
3. Предельные значения процента армирования балок
4. Оптимальный процент армирования прямоугольных балок и плит
5. Таблицы для расчета плит и балок прямоугольного сечения с одиночной арматурой
6. Примеры расчета прямоугольных сечений балок с одиночной арматурой
Б. Прямоугольная балка или плита с двойной арматурой
1. Формулы для определения Mp
2. Армирование при различном соотношении площадей сжатой и растянутой арматуры. Армирование при условии min (Fa + F’a)
Армирование при различном соотношении площадей сжатой и растянутой арматуры. Армирование при условии min (Fa + F’a)
3. Примеры расчета плит и балок с двойной арматурой
B. Балка таврового сечения
1. Работа тавровой балки на изгиб
2. Наименьший процент армирования растянутой зоны балок таврового сечения
3. Расчет балок таврового сечения на отрицательный момент
4. Расчет балок таврового сечения на положительный момент
5. Выбор высоты балок таврового сечения
6. Примеры расчета балок таврового сечения
Глава V. Расчет и конструирование арматуры плит перекрытий (балочные плиты и плиты, опертые по контуру)
1. Конструктивные указания по проектированию балочных плит и плит, опертых по контуру
2. Пример расчета и конструирования балочных плит ребристого перекрытия
3. Пример расчета и конструирования плиты кессонного перекрытия
Глава VI. Расчет изгибаемых элементов, на поперечную силу
1. Работа балок при поперечном срезе по данным опытов
Работа балок при поперечном срезе по данным опытов
2. Скалывающие напряжения и главные напряжения в балке
3. Расчетные эпюры σгл = τ вдоль балки
4. Оценка по эпюре σгл = σ сопротивляемости балки главным растягивающим напряжениям. Распределение эпюры на части с передачей их на продольную арматуру, хомуты и косые стержни
5. Расчет и конструирование хомутов
6. Расчет и конструирование отогнутой арматуры
7. Эпюра арматуры. Прочность балки по нормальным и косым сечениям
Глава VII. Расчет и конструирование балок по изгибу и поперечному срезу
1. Конструктивные указания по проектированию балок
2. Пример расчета и конструирования однопролетных свободно лежащих балок с равномерно распределенной нагрузкой
3. Пример расчета и конструирования однопролетных свободно лежащих балок под действием сосредоточенных сил
4. Пример расчета и конструирования неразрезных балок ребристого перекрытия
5. Применение вутов в неразрезных балках ребристого перекрытия
Глава VIII.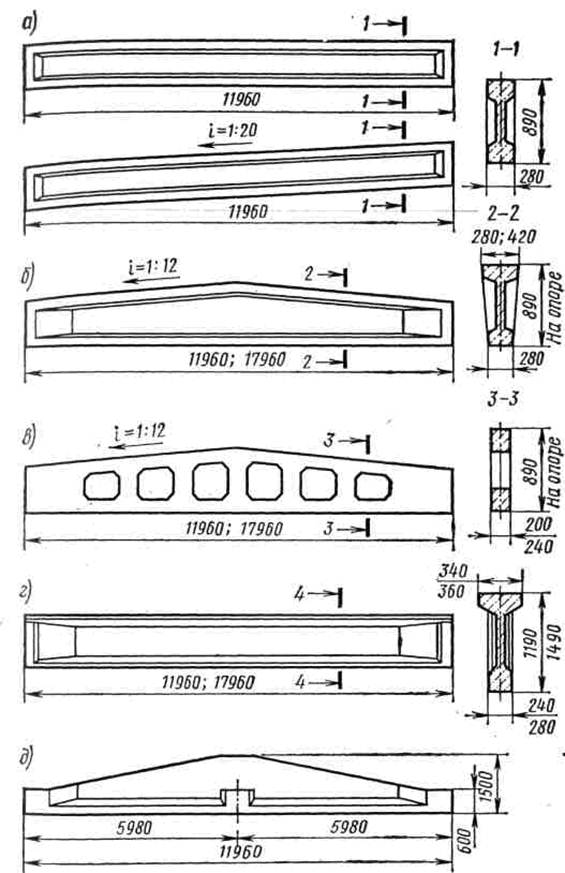 Консоли, их расчет и конструирование
Консоли, их расчет и конструирование
1. Примеры применения консолей в строительстве
2. Расчет и конструирование консолей с большим вылетом
3. Расчет и конструирование коротких консолей
Глава IX. Расчет изгибаемых элементов, к которым предъявляются требования непроницаемости бетона
1. Изгибаемые элементы с обыкновенной арматурой и с арматурой, имеющей предварительное натяжение
А. Расчет на изгиб бетонных неармированных балок
2. Расчет бетонных неармированных балок на изгиб по ТУ и Н проектирования бетонных конструкций (ОСТ 90040—39)
3. Расчет бетонных неармированных балок на изгиб по стадии напряженности IIa
Б. Расчет на изгиб железобетонных балок с обыкновенной арматурой
4. Расчет железобетонных балок на изгиб по стадии напряженности I
5. Расчет на изгиб железобетонных балок прямоугольного сечения с одиночной или с двойной арматурой по стадии напряженности IIa
6. Расчет на изгиб железобетонных балок прямоугольного сечения по стадии напряженности IIb
7. Примеры расчета и сопоставление различных приемов расчета
Примеры расчета и сопоставление различных приемов расчета
В. Расчет на изгиб балок с предварительно напряженной арматурой
8. Определение Mm для балок прямоугольного сечения с двойной арматурой, имеющей предварительное натяжение
9. Определение Mm для балок прямоугольного сечения с одиночной или двойной арматурой, часть стержней которой имеет предварительное натяжение
10. Потеря арматурой первоначального (монтажного) напряжения
11. Сравнение результатов расчета по выведенным формулам с опытными данными для железобетонных балок прямоугольного сечения с одиночной арматурой, имеющей предварительное натяжение
12. Графики и таблицы для расчета Mm. Примеры расчёта на изгиб балок с предварительно напряженной арматурой
13. Расчет на положительный момент балок таврового сечения с арматурой, имеющей предварительное натяжение
Раздел II. Осевое и внецентренное сжатие
Глава X. Элементы железобетонных конструкций, работающие на осевое и внецентренное сжатие (колонны и стойки, рамные и арочные конструкции)
1. Общие сведения
Общие сведения
2. Конструкции, работающие на осевое и внецентренное сжатие
Глава XI. Осевое сжатие
А. Колонны с продольной арматурой и обыкновенными хомутами
1. Расчет коротких колонн с продольной арматурой и обыкновенными хомутами
2. Конструктивные указания по проектированию на осевое сжатие колонн с продольной арматурой и обыкновенными хомутами
3. Продольный изгиб и его учет в расчетах прочности колонн
4. Примеры расчета колонн на осевое сжатие с продольной арматурой и обыкновенными хомутами
Б. Колонны со спиральной арматурой
5. Расчетные формулы и их обоснование
6. Конструктивные указания по проектированию «бетона в обойме»
7. Примеры расчета и конструирования колонн со спиральной арматурой («бетона в обойме»)
Глава XII. Внецентренное сжатие колонн и стоек прямоугольного сечения с продольной арматурой и обыкновенными хомутами
1. Общие предпосылки к расчету внецентренно сжатых сечений.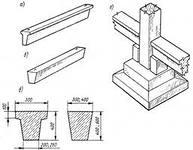 Принятые обозначения
Принятые обозначения
2. Расчетные формулы для первого случая внецентренного сжатия
3. Расчетные формулы для второго случая внецентренного сжатия
4. Указания по конструированию и расчету внецентренно сжатых элементов
5. Учет гибкости колонн и стоек при расчете их на внецентренное сжатие
6. Примеры подбора сечений внецентренно сжатых элементов
7. Расчет на внецентренное сжатие элементов таврового сечения
8. Расчет на внецентренное сжатие при соблюдении требования непроницаемости бетона
Раздел III. Осевое и внецентренное растяжение
Глава XIII. Элементы конструкций, работающие на осевое и внецентренное растяжение
Глава XIV. Осевое растяжение
1. Расчет прочности при осевом растяжении
2. Расчет, обеспечивающий требование непроницаемости бетона
3. Мероприятия, предотвращающие образование волосных трещин в бетоне растянутых элементов конструкции
Глава XV. Внецентренное растяжение
1. Первый случай внецентреиного растяжения
Первый случай внецентреиного растяжения
2. Второй случай внецентреиного растяжения
3. Примеры расчета сечений на внецентренное растяжение
4. Расчет на внецентренное растяжение при соблюдении требования непроницаемости бетона
Раздел IV. Кручение в железобетоне
Глава XVI. Опыты и расчеты
1. Возникновение крутящих моментов в элементах конструкции и учет их в расчетах
2. Кручение бетонных круглых цилиндрических образцов. Определение σгл = τкр. Опытные данные
3. Кручение бетонных элементов прямоугольного сечения. Определение σгл = τкр
4. Армирование железобетонных элементов при кручении. Расчетные формулы. Пример расчета
5. Опытные данные при кручении армированных образцов
6. Совместное действие кручения и изгиба
Приложения
Приложение 1. Таблицы для статического расчета железобетонных конструкций
A. Таблица для расчета на изгиб плит, опертых по контуру, при сплошной равномерно распределенной нагрузке q
Б. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной p
Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной p
B. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при сосредоточенной нагрузке: постоянной G и временной P
Г. Таблица пролетных и опорных моментов и поперечных сил в опорных сечениях неразрезных балок с равными пролетами
Д. Таблица опорных моментов для неразрезных балок с равными пролетами и постоянного сечения при любых нагрузках, симметричных по отношению к пролету. Концы балок могут быть свободно положены на опоры (схема I) или жестко заделаны в опорах (схема II)
Е. Таблица грузовых коэфициентов s балок с симметричной нагрузкой
Ж. Таблица моментов, поперечных сил и эквивалентных по моменту нагрузок для свободно лежащих балок
З. Таблица моментов в равнопролетной балке на упруго вращающихся опорах
Приложение 2. Таблицы и графики для расчета элементов железобетонных конструкций
Iа. Таблица круглого железа
Таблица круглого железа
I6. Таблица площадей арматуры в 1 пог. м плиты при различном расстоянии между стержнями
II. Таблица для расчета на изгиб плит и балок прямоугольного сечения с одиночной арматурой
III. Таблица для подбора прямоугольных сечений с одиночной арматурой
IV. График для расчета прямоугольных сечений на изгиб
V. Таблица для подбора сечений на изгиб с одиночной или двойной арматурой и на внецентренное сжатие и растяжение
VI. а, б, в, г, д. Графики расчета Mm для балок прямоугольного сечения с одиночной арматурой
VII. Таблица для подбора внецентренно сжатых прямоугольных сечений с двойной симметричной арматурой
VIII. График значении n1 = Np / Rubh в зависимости от c0 = e0 / h и σ1 = α’1 = σmFα / Rubh при внецентренном сжатии прямоугольных сечении с двойной симметричной арматурой при δ1 = 0,08
IX. График для расчета внецентренно сжатых элементов прямоугольного сечения (δ1 = δ’1 = 0,08)
X.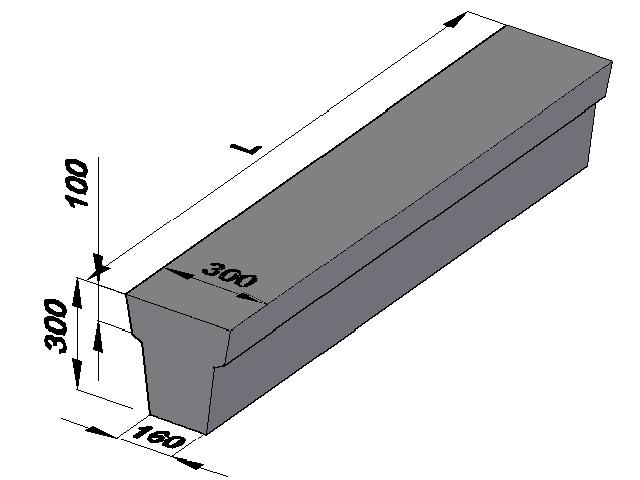 а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой
а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой
XI. График для определения моментов инерции тавровых сечений
XII. График для определения коэфициента m при расчете внецентренно сжатых сечений с учетом гибкости элемента
XIIIa. Таблица для расчета на изгиб балок прямоугольного сечения с предварительно напряженной арматурой. Марка бетона 250 кг/см2
XIIIб. То же. Марка бетона 300 кг/см2
XIIIв. То же. Марка бетона 350 кг/см2
Приложение 3. Принятые обозначения
Приложение 4. Свод формул и правил расчета и конструирования железобетонных элементов
Предисловие
Современный курс железобетонных конструкций, отражая с максимальной полнотой достижения в области теории железобетона, должен также достаточно удовлетворять запросам практики.
Совершенно очевидно также, что в курсе должна быть дана и перспектива развития теории и практики железобетона.
Автор не считает, что в этой книге с достаточной полнотой получили разрешение перечисленные выше задачи. Материал, использованный при написании данной второй части курса, настолько обширен, многообразен и по существу нов, что некоторые положения, приведенные в курсе, нуждаются еще в серьезной дополнительной теоретической и экспериментальной проверке.
Насущные потребности текущей учебной и производственной практики однако столь важны и неотложны, что автор не счел возможным откладывать написание курса впредь до окончания разработки этих положений.
Все указания и пожелания читателей, касающиеся улучшения качества книги, будут приняты автором с благодарностью и учтены при переиздании книги.
Вторая часть курса, в которой излагаются расчет и конструирование элементов железобетонных конструкций, построена на базе действующих ТУ и Н 1939 г. (ОСТ 90003—38). Применительно к этим нормам, с использованием теоретического и экспериментального материала ЦНИПС и других научно-исследовательских организаций, нашей и иностранной технической литературы, а также личных исследований автора построено изложение курса.
При составлении курса была также учтена «Инструкция по применению норм и технических условий проектирования железобетонных конструкций», которая разрабатывалась во время написания книги.
Расположение материала в книге, трактующей о сопротивляемости железобетонных элементов при различном воздействии усилий, соответствует в основном обычно принятому расположению материала в курсе сопротивления материалов.
Раздел I курса излагает сопротивляемость железобетона изгибу и скалыванию при изгибе; здесь же приведены данные по расчету и конструированию таких элементов.
В разделе II рассмотрены вопросы расчета и конструирования элементов, работающих на осевое и внецентренное сжатие.
В раздел III вошли главы, посвященные осевому и внецентренному растяжению.
Раздел IV посвящен вопросам расчета и конструирования при наличии кручения в элементах конструкции.
Все изложение теоретических вопросов сопровождается примерами расчета и конструирования. Для облегчения расчетов даются графики и таблицы.
Каждому разделу предшествует обзор применяемых в практике конструкций.
Одним из недочетов новых норм является отсутствие в них указаний по расчету изгибаемых, внецентренно сжатых и внецентренно растянутых элементов, к которым предъявляются требования непроницаемости бетона. Этот пробел устранен в курсе. Все указания по этим расчетам, сопровождаемые графиками, таблицами и примерами практического применения, изложены достаточно полно. Кроме того уделено внимание расчету изгибаемых элементов с предварительно напряженной арматурой.
В заключение автор считает своим долгом принести глубокую благодарность доктору технических наук проф. В.М. Келдыш за его ценные указания при написании книги и при ее рецензировании, а также доктору технических наук проф. А.А. Гвоздеву за его ценные замечания при рецензировании книги.
Проф. В. Бушков
Балки таврового сечения — презентация онлайн
1. Лекция №5
Балки таврового сеченияВопросы, подлежащие изучению:
1.
2.
Общие сведения о балках таврового сечения.
Расчет ж/б элементов таврового сечения.
1. Общие сведения о балках таврового сечения
Целесообразность применения тавровой формы сечения
ж/б элементов обусловлена тем, что в таком сечении сводится
к минимальной площадь неработающего растянутого бетона,
но развита рабочая сжатая зона.
b f
b b Rb
полка
h f
ее
свес
h
е
h0
a
ребро
As
b
е – е — скалывание
Чтобы свесы были напряжены
одинаково, в расчет вводят
эквивалентную ширину свесов:
b f bб
— шаг балок
b f ; — пролет
3
Нормы ограничивают размеры полки или свеса, чтобы
исключить разрушение по сечению от скалывающих
усилий и чтобы точнее учесть расчетом работу свесов
(см. выше).
1. При h f 0,1h
b f 12h f b
2. При 0,05h h f 0,1h
b f 6h f b
3. Если
h f 0,05h полки расчетом не учитываются.
2. Расчет ж/б элементов таврового сечения
Различают 2 случая расчета.

Случай 1. Сжатая зона сечения находится выше ребра,
т.е. Н.Л. проходит в пределах полки ( x h f ).
Это бывает, когда M M f воспринимаемого сжатой полкой и растянутой арматурой, относительно центра тяжести
растянутой арматуры. M f — «момент полки».
b f
1
x
н.л.
h
h0
As
a
h f
Rs As Rb b f h f
M M f Rbb f h f (h0
h f
2
)
M Rbb f h02 m
b
В этом случае расчет производится по формуле балки прямоугольного
сечения, в котором величина b заменяется на b f
Случай 2. Сжатая зона сечения опускается ниже
полки ( x h f ), т.е. Н.Л. пересекает ребро. Расчет
проводят с учетом сжатия в ребре.
b f
2
h f
h
x
н.л.
h0
a
As
b
Такой случай определяется
выражением
M M f Rb b f h f (h0 0,5h f )
Расчет производят в следующем порядке: раскладывают
несущую способность тавра на несущую способность ребра
и несущую способность свесов.
M OV
M1
M
x
x
h0
h0
As1
a
As 2
x
h f
2
As
M M 1 M OV
As As1 As 2
AOV – площадь свесов
AOV h f (b f b)
M OV Rb AOV (ho 0,5h f )
As 2
M OV
Rs ( h0 0,5h f )
Момент в ребре M 1 M M OV
M
R bh
1
m
b
2
0
As1 Rbbh0 (1 1 2 m ) / Rs
As As1 As 2
Методика проектирования железобетонной тавровой балки с примером
Тавровые балки образуются при монолитном отливке железобетонных плит перекрытия, крыш и настилов с помощью поддерживающих балок. Как правило, опалубки устанавливаются на днище и боковые стороны балок и перекрытия перекрытий. Загнутые вверх стержни и хомуты балки выдвигаются вверх в плиту. После этого отливаются сразу все элементы, от самой нижней точки балки до верха плиты.
Часть плиты вокруг балки, называемая фланцем, будет работать с балкой и противостоять силе продольного сжатия.Внутренние балки имеют фланцы с обеих сторон и называются Т-образными балками, а краевые балки имеют фланцы с одной стороны и называются L-образными балками. Часть балки, проходящая под плитой, называется стержнем или стенкой.
Часть балки, проходящая под плитой, называется стержнем или стенкой.
Конструкция железобетонных тавровых балок аналогична конструкции прямоугольной железобетонной балки, за исключением полок, которые необходимо учитывать в балках первого типа.
Эффективная ширина фланца
Для начала процесса проектирования необходимо определить эффективную ширину полки (b e ) тавровой балки.На Рисунке 1 фланец изолированной Т-образной балки немного шире, чем шток Т-образной балки, и весь фланец эффективно противостоит сжатию.
Рисунок 1: Эффективная ширина полки изолированной тавровой балкиОднако на рисунке 2 ширина фланца велика; следовательно, части фланцев, расположенные на расстоянии от штока, не принимают на себя полную долю сопротивления сжатию, и напряжения продолжают изменяться.
Рисунок 2: Эффективная ширина полки внутренней тавровой балки Изменение напряжений приводит к утомительным вычислениям; вот почему равномерное распределение напряжений рассматривается на меньшей ширине рабочего фланца, см. Рисунок-3.
Рисунок-3.
Согласно ACI 318-19, эффективная ширина полки Т-образной балки может быть найдена следующим образом:
1. Изолированные балки
Для изолированных балок, в которых фланец используется только для обеспечения дополнительной зоны сжатия, фланец должен иметь толщину не менее 1 / 2b w, и эффективную ширину не менее 4b w .
Рисунок 4: Геометрия изолированной тавровой балки2. Балка внутренняя тавровая
Согласно 318-19, эффективная ширина полки внутренней тавровой балки не должна превышать наименьшее из:
1- Одна четвертая длины пролета балки, L / 4.
2- Ширина стенки плюс 16-кратная толщина плиты, b w + 16h f .
3- Расстояние между центрами балок.
3.
 Краевая балка (L-образная)
Краевая балка (L-образная)Согласно 318-19, эффективная ширина полки краевой балки не должна превышать наименьшее из:
1- Эффективная ширина фланца (b e ), равная или меньше (b w + (Чистый диапазон / 4))
2- Эффективная ширина фланца (b e ) не более (b w + (6h f )
3- Эффективная ширина полки (b e ), равная или меньшая (b w + половина свободного расстояния до следующей чистой перемычки)
Рисунок 6: Эффективная ширина полки L-образной балкиТавровая балка и прямоугольная балка
Если Т-образная железобетонная балка подвергается воздействию отрицательных моментов на опорах, балка проектируется как прямоугольное сечение, так как бетон, находящийся на растяжение, не учитывается.Ширина прямоугольного сечения равна ширине ствола (стенки), см. Рисунок 7.
Рисунок 7: Т-образная балка подвергается отрицательному моменту Однако, когда на тавровую балку действует положительный момент, фланец находится в зоне сжатия, поэтому балка должна быть спроектирована как тавровая балка, см. Рисунок-8.
Рисунок-8.
Проектирование Т-балки железобетонной
Расчет балки с Т-образным сечением включает расчет размеров (be, h f , h и b w ) балки и требуемой площади армирования (As).Толщина полки (h f ) и ширина (b e ) обычно устанавливаются при проектировании плиты.
На размер стенки или стержня балки влияют те же факторы, что и на размер прямоугольной балки. В случае неразрезной тавровой балки сжимающие напряжения бетона наиболее критичны в областях с отрицательным моментом, где зона сжатия находится в стержне (стенке) балки.
Распределение напряжений в тавровой балке показано на Рисунке 9:
. Рисунок 9: Распределение напряжений в тавровой балкеПроцедура проектирования
- Рассчитайте приложенный момент (M и ), используя пролет балки и приложенные нагрузки.
2. Определите эффективную ширину фланца (b e )
3. Выберите размеры стенки (b w ) и (h) на основании требований к отрицательному изгибу на опорах или требований к сдвигу.
Выберите размеры стенки (b w ) и (h) на основании требований к отрицательному изгибу на опорах или требований к сдвигу.
4. Предположим, что a = h f , затем вычислим (As), используя следующее выражение:
5. Проверьте предполагаемое значение (a):
В уравнении 2 подставьте значение (b e ), найденное на шаге 2.
Если a Если a> hf, спроектируйте балку Т-образным сечением и переходите к этапу 6. 6. Рассчитайте площадь армирования, необходимую для уравновешивания момента фланца, используя уравнение 3, а затем момент фланца используйте уравнение 4: 7. Рассчитать момент в сети: 8. Предположите, что глубина прямоугольного блока напряжений (например, a = 100 мм), затем оцените величину площади армирования (A sw ), необходимую для уравновешивания момента стенки: Значение (d) следует рассчитать по следующей формуле: d = высота балки — бетонное покрытие — диаметр хомутов — 0. Затем проверьте предполагаемую глубину прямоугольного напряженного блока (a), используя (A sw ): Используйте новый (a) и вставьте его в уравнение 6, затем вычислите новое (A sw ). Повторяйте этот процесс, пока не будет достигнуто правильное значение (A sw ). Обычно достаточно трех попыток. 9. Вычислить сумму As, равную (A sf + A sw ), затем определить количество армирования: №Кол-во стержней = As / площадь одного стержня Уравнение 9 10. Набросайте окончательный эскиз, на котором представлены все необходимые данные. Где: Система перекрытий, показанная на Рисунке 10, состоит из бетонной плиты толщиной 75 мм, поддерживаемой бетонными Т-образными балками с пролетом 7,5 м и центрами 1,2 м. Размеры перемычки, которые определяются требованиями к отрицательным моментам на опорах, составляют b w = 275 мм и d = 500 мм. 1. Прилагаемый момент предусмотрен, Mu = 725 кН.м 2. Найдите эффективную ширину фланца (b e ), которая является наименьшей из следующих величин: Следовательно , эффективная ширина фланца равна 1200 мм. 3. Приведены размеры полотна. 4. Предположим, что a = h f = 75 мм, и предположим, что коэффициент уменьшения прочности равен 0,9. As = (725 * 10 6 ) / (0,9 * 420 (500-0,5 * 75) = 4147,004 мм 2 5. Проверьте предполагаемое значение (a), используйте (As), вычисленное на шаге 4: a = (4147,004 * 420) / (0,85 * 21 * 1200) = 81,31 мм Поскольку a = 81,31 мм> hf = 75 мм, балка должна иметь Т-образное сечение. 6. Вычислить (A SF ) и момент фланца: A SF = (0,85 * 21 * (1200-275) * 1200) / 420 = 2946,23 мм 2 фи * M nf = 2946,23 * 420 * (500-0,5 * 75) * 10 -6 = 572,23 кН.м 7. Рассчитать момент в сети: phi * M nw = 725-572,23 = 209,54 кН.м 8. Оцените площадь армирования (A sw ), предположив, что a = 100 мм и phi = 0.9 A sw = (209,54 * 10 6 ) / (0,9 * 420 * (500-0,5 * 100) = 1231,86 мм 2 проверьте (a) используя вышеуказанное (A sw ), a = (1231,86 * 420) / (0,85 * 21 * 275) = 105,4 мм Найдите новый (A sw ) используйте a = 105,4 мм A sw = (209,54 * 10 6 ) / (0,9 * 420 * (500-0,5 * 105,4) = 1239,29 мм 2 Поскольку новый A sw очень близок к предыдущему, дальнейшие испытания не требуются. A sw = 1239,29 мм 2 9. Вычислить общую сумму As, равную (A sf + A sw ): As = A SF + A sw = 2946,23 + 1239,29 = 4180,29 мм 2 Следует проверить предполагаемый коэффициент снижения прочности: Выбор одного стального стержня приводит к тому, что площадь армирования значительно превышает общую площадь. Следовательно, нет. 32 и нет.Отобрано 29 стальных стержней для получения площади армирования, максимально приближенной к требуемой площади армирования. Имеется три стержня диаметром 32 мм, и соответствующая площадь армирования составляет 2457 мм 2 Имеется три стержня диаметром 29 мм, и соответствующая площадь армирования составляет 1935 мм 2 Общая площадь армирования равна 4349 мм 2 ; , это и есть ответ на вопрос. Итак, стальные стержни укладываются в два слоя, расстояние между двумя слоями составляет 25 мм. Проверить коэффициент снижения прочности: Так как прочность бетона на сжатие меньше 30 МПа, то B 1 = 0,85 глубина нейтральной оси (c) = a / B 1 = 105,4 / 0,85 = 124 мм dt: расстояние от сжатой поверхности балки до центра нижнего слоя стальных стержней: c / dt = 124/525 = 0.236 <0,375. Следовательно, предположение верное. Для получения более подробной информации о расчете коэффициента снижения прочности нажмите здесь Как правило, система перекрытия из железобетона состоит из балок и плиты, которые построены монолитно. В результате части плиты вокруг верхней части балки работают вместе, чтобы нести нагрузки. Фактически, балки имеют дополнительную ширину в верхней части, которая называется полками. Эффективная ширина полки складывается из стенки балки плюс ширина полки с каждой стороны балки. Распределение напряжения по ширине эффективной ширины фланца равномерное. Эффективная глубина равна расстоянию от сильно сжатого волокна балки до центра тяжести стальных стержней, встроенных в балку. Подробнее Расчет прямоугольной железобетонной балки Основы проектирования балок Имя пользователя* Электронное письмо* Пароль* Подтвердить Пароль* Имя* Фамилия* Страна Выберите страну … Аландские острова IslandsAfghanistanAlbaniaAlgeriaAndorraAngolaAnguillaAntarcticaAntigua и BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelauBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Санкт-Эстатиус и SabaBosnia и HerzegovinaBotswanaBouvet IslandBrazilBritish Индийского океана TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral африканского RepublicChadChileChinaChristmas IslandCocos (Килинг) IslandsColombiaComorosCongo (Браззавиль) Конго (Киншаса) Кук IslandsCosta RicaCroatiaCubaCuraÇaoCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland IslandsFaroe IslandsFijiFinlandFranceFrench GuianaFrench PolynesiaFrench Южный Территорий нг КонгВенгрияИсландияИндияИндонезияИранИракОстров ЧеловекаИзраильИталия Кот-д’ИвуарЯмайкаЯпонияДжерсиИорданияКазахстанКенияКирибатиКувейтКиргизияЛаосЛатвияЛебанЛезотоЛиберияЛибияЛихтенштейнЛихтенштейнЛитва ЮжныйAR, ChinaMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth KoreaNorwayOmanPakistanPalestinian TerritoryPanamaPapua Новый GuineaParaguayPeruPhilippinesPitcairnPolandPortugalQatarRepublic из IrelandReunionRomaniaRussiaRwandaSão Tomé и PríncipeSaint BarthélemySaint HelenaSaint Китса и NevisSaint LuciaSaint Мартин (Голландская часть) Сен-Мартен (французская часть) Сен-Пьер и MiquelonSaint Винсент и GrenadinesSan MarinoSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Грузия / Sandwich ОстроваЮжная КореяЮжный СуданИспанияШри-ЛанкаСуданСуринамШпицберген и Ян-МайенСвазилендШвецияШвейцарияСирияТайваньТаджикистанТанзанияТаиландТимор-ЛештиТогоТокелауТонгаТринидад и ТобагоТунисТурция ТуркменистанТуркс и Острова КайкосТувалуУгандаУкраинаОбъединенные Арабские ЭмиратыВеликобритания (Великобритания) США (США) УругвайУзбекистанВануатуВатиканВенесуэлаВьетнамУоллис и ФутунаЗападная СахараЗападное СамоаЙеменЗамбияЗимбабве Регистрируясь, вы соглашаетесь с Условиями использования и Политикой конфиденциальности. Имя пользователя* Электронное письмо* Пароль* Подтвердить Пароль* Имя* Фамилия* Страна Выберите страну … Аландские острова IslandsAfghanistanAlbaniaAlgeriaAndorraAngolaAnguillaAntarcticaAntigua и BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelauBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Санкт-Эстатиус и SabaBosnia и HerzegovinaBotswanaBouvet IslandBrazilBritish Индийского океана TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral африканского RepublicChadChileChinaChristmas IslandCocos (Килинг) IslandsColombiaComorosCongo (Браззавиль) Конго (Киншаса) Кук IslandsCosta RicaCroatiaCubaCuraÇaoCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland IslandsFaroe IslandsFijiFinlandFranceFrench GuianaFrench PolynesiaFrench Южный Территорий нг КонгВенгрияИсландияИндияИндонезияИранИракОстров ЧеловекаИзраильИталия Кот-д’ИвуарЯмайкаЯпонияДжерсиИорданияКазахстанКенияКирибатиКувейтКиргизияЛаосЛатвияЛебанЛезотоЛиберияЛибияЛихтенштейнЛихтенштейнЛитва ЮжныйAR, ChinaMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth KoreaNorwayOmanPakistanPalestinian TerritoryPanamaPapua Новый GuineaParaguayPeruPhilippinesPitcairnPolandPortugalQatarRepublic из IrelandReunionRomaniaRussiaRwandaSão Tomé и PríncipeSaint BarthélemySaint HelenaSaint Китса и NevisSaint LuciaSaint Мартин (Голландская часть) Сен-Мартен (французская часть) Сен-Пьер и MiquelonSaint Винсент и GrenadinesSan MarinoSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Грузия / Sandwich ОстроваЮжная КореяЮжный СуданИспанияШри-ЛанкаСуданСуринамШпицберген и Ян-МайенСвазилендШвецияШвейцарияСирияТайваньТаджикистанТанзанияТаиландТимор-ЛештиТогоТокелауТонгаТринидад и ТобагоТунисТурция ТуркменистанТуркс и Острова КайкосТувалуУгандаУкраинаОбъединенные Арабские ЭмиратыВеликобритания (Великобритания) США (США) УругвайУзбекистанВануатуВатиканВенесуэлаВьетнамУоллис и ФутунаЗападная СахараЗападное СамоаЙеменЗамбияЗимбабве Регистрируясь, вы соглашаетесь с Условиями использования и Политикой конфиденциальности. Имя пользователя* Электронное письмо* Пароль* Подтвердить Пароль* Имя* Фамилия* Страна Выберите страну … Аландские острова IslandsAfghanistanAlbaniaAlgeriaAndorraAngolaAnguillaAntarcticaAntigua и BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelauBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Санкт-Эстатиус и SabaBosnia и HerzegovinaBotswanaBouvet IslandBrazilBritish Индийского океана TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral африканского RepublicChadChileChinaChristmas IslandCocos (Килинг) IslandsColombiaComorosCongo (Браззавиль) Конго (Киншаса) Кук IslandsCosta RicaCroatiaCubaCuraÇaoCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland IslandsFaroe IslandsFijiFinlandFranceFrench GuianaFrench PolynesiaFrench Южный Территорий нг КонгВенгрияИсландияИндияИндонезияИранИракОстров ЧеловекаИзраильИталия Кот-д’ИвуарЯмайкаЯпонияДжерсиИорданияКазахстанКенияКирибатиКувейтКиргизияЛаосЛатвияЛебанЛезотоЛиберияЛибияЛихтенштейнЛихтенштейнЛитва ЮжныйAR, ChinaMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth KoreaNorwayOmanPakistanPalestinian TerritoryPanamaPapua Новый GuineaParaguayPeruPhilippinesPitcairnPolandPortugalQatarRepublic из IrelandReunionRomaniaRussiaRwandaSão Tomé и PríncipeSaint BarthélemySaint HelenaSaint Китса и NevisSaint LuciaSaint Мартин (Голландская часть) Сен-Мартен (французская часть) Сен-Пьер и MiquelonSaint Винсент и GrenadinesSan MarinoSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Грузия / Sandwich ОстроваЮжная КореяЮжный СуданИспанияШри-ЛанкаСуданСуринамШпицберген и Ян-МайенСвазилендШвецияШвейцарияСирияТайваньТаджикистанТанзанияТаиландТимор-ЛештиТогоТокелауТонгаТринидад и ТобагоТунисТурция ТуркменистанТуркс и Острова КайкосТувалуУгандаУкраинаОбъединенные Арабские ЭмиратыВеликобритания (Великобритания) США (США) УругвайУзбекистанВануатуВатиканВенесуэлаВьетнамУоллис и ФутунаЗападная СахараЗападное СамоаЙеменЗамбияЗимбабве Регистрируясь, вы соглашаетесь с Условиями использования и Политикой конфиденциальности. 1.8 Расстояние между арматурой и бетонным покрытием Расстояние между арматурой и бетонным покрытием должно
быть достаточным, чтобы облегчить бетонирование; следовательно, бетон
окружающая арматура может эффективно вибрировать, что приводит к плотному
бетонное покрытие, обеспечивающее подходящую защиту арматуры от
коррозия. 1.8.1 Расстояние между арматурой Рисунок
1.19
показаны два железобетонных разреза. Полосы размещены таким образом, чтобы
расстояние с должно быть не менее максимального диаметра стержней, или
25 мм, или в 1,50 раза больше максимального размера заполнителя, в зависимости от того, что больше, в зависимости от
к Египетскому кодексу. Вертикальное расстояние между стержнями, более одного
слой, должен быть не менее 25 мм. РИСУНОК 1.19 Расстояние между стальными стержнями
а) в один ряд или б) в два ряда. 1.8.2 Бетонное покрытие Указанный
минимальное бетонное покрытие для различных элементов конструкции в соответствии с их
степень воздействия указана в Египетских Кодексах, Таблица 4-13. Бетонное покрытие
для балок равен 25 мм для основных стержней и 20 мм для хомутов, а для
плиты равны 15 мм, когда бетон не подвергается атмосферным воздействиям или контакту
с землей. 1.8.3 Количество стальных слоев и
Общая глубина бетонной секции Генерал
уравнение для требуемой ширины бетонного сечения выглядит следующим образом: ( 1,55 ) The
общая глубина t равна эффективной глубине d плюс расстояние
от центра тяжести растянутой арматуры до бетона с предельным напряжением
волокна, что зависит от количества слоев стальных стержней.В приложении
в разрез, показанный на рис. за один ряд
стальные прутки и для двух слоев
стальных прутков, рис.1.19b. Глубина габаритная т. довести до
ближайшие 5 см. Если используются стержни № 8 (25 мм) или меньше, практическая оценка
общей глубины можно сделать следующим образом: т = d + 50 мм, для одного слоя прутков т = d + 75 мм, для двух слоев стальных стержней Пример 1.4: Для консольной балки, показанной на рис.
1.20, если DL = 13,5 кН / м ‘(включая собственный вес) и LL = 35 кН, необходимо: а. Расчет секции балки на минимальную глубину, когда b = 250 мм. б. Расчет секции балки на минимальную глубину, когда b = 120 мм. c. Расчет секции балки на эффективную глубину d = 450 м при b = 250 мм. d. Расчет секции балки на общую глубину т = 700 м при b = 120 мм. Дано: = 25 Н / мм2 и = 280 Н / мм2. РИСУНОК 1.20. Пример 1.4. Решение: Окончательный
момент как указано в Египетском кодексе (где и мертвые и живые моменты службы соответственно)
быть: Часть A: Войти в таблицу
A.1 с f cu =
25 Н / мм2
и = 280 Н / мм2
и получаем = 0,534 и = 196,7 Тогда,
вычислить
и следующим образом: Для = 1842 мм2,
различные варианты стальных стержней могут быть выбраны следующим образом: Стальной пруток Площадь стали ,
мм2 1884 Площадь
стальные стержни должны располагаться как можно ближе к требуемой стальной поверхности. 2
f 25 плюс 2 f 22 необходимо разместить в один ряд, так как ширины 250 мм достаточно.Расчет необходимой ширины для размещения 2 f
25 плюс 2 ж
22 в один слой: = 2 (f25 + 22f22) + 3 s + 2f str + 2 c знак равно
2 (25 + 22) + 3 25 + 2
8 + 2
25 = 235 мм что меньше
чем b = 250 мм. Общая глубина т затем вычисляется по формуле: т = д + 0.5f25 + f ул. + с = 414 + 0,5 25 + 8 + 25 =
461,5 мм; скажем, 500 мм Фактический
эффективная глубина d = 500-50 = 450 мм , который
больше расчетного d на 414 мм. что меньше
чем 1740 мм2 (2
ж 25 плюс 2 ж 22)
при условии, рис. 1.21. РИСУНОК 1.21 Пример 1.4, часть а. Часть b: Минимум
эффективная глубина, соответствующая b = 120 мм, равна 597.5 мм. Площадь
из стали A s требуется
равно A smax или 1276 мм2.
Если 4 f
20 выбрано, A s =
1256 мм2,
что на 20 мм2 меньше
чем 1276 мм2.
Если стальные стержни расположены в один ряд: = 4 20 + 3
25 + 2 8 + 2 25 = 211
мм , который
больше b = 120 мм, поэтому стальные стержни должны быть размещены в
двух рядов шириной 120 мм недостаточно. t = 597,5 + 25 + 8 + 20 + 0,5 25 = 663 см; сказать
700 мм Фактический d = 700 — 75 = 625 мм РИСУНОК 1.22 Пример 1.4, часть b. Часть c: Первая
рассчитать K 1
с: , что дает К 1 =
0.581. Войти в таблицу
B.2 с K 1 =
0,581, затем двигайтесь по горизонтали до = 25, и в итоге получаем A smin =
наименьшее из: 1. Но не менее А smin = 442 мм2 А smax =
1968,75 мм2 Здесь, 1630 мм2, что
больше A smin и меньше чем . 163 мм2
(Используйте 2 f 12) Часть d: Если предполагается сталь
укладывать в два слоя, так как ширины 120 мм недостаточно. д = 600
— 75 = 525 мм Первая
рассчитать K 1
с: Войти в таблицу
B.2 с K 1 =
0,468, первое значение К 1
(которые соответствуют = 25) составляет 0,534, что больше 0,468. С меньше 0.20, \ . 1.9 Фланцевый
Разделы Бетонный пол
плиты и балки обычно связываются между собой стременами и изогнутыми стержнями
если таковые имеются, а затем отливаются в одну массу бетона. Такая монолитная система
будет действовать как единое целое, т. е. можно предположить, что часть плиты действует
с балкой, и они образуют так называемую фланцевую балку, рис. РИСУНОК 1.23 Балочный перекрытие
система. Часть
плита, взаимодействующая с балкой, называется полкой и обозначена на рис.
1.24a площадью Bt s .
Остальная часть участка ограничивающая площадь ( т-т с ) б называется стержнем или сеткой. Как показано на рис. 1.24b, на участке I имеется
два фланца, компрессионный фланец, который действительно эффективен, и
натяжной фланец, который неэффективен, поскольку находится ниже нейтральной оси и
таким образом, полностью игнорируется.Следовательно, конструкция профиля I аналогичен профилю T . РИСУНОК 1.24 (a) T — разрез
и (b) I — раздел. 1.9.1 Эффективно
Ширина фланца, B Как Рис.
1,25
указывает, что сжимающие напряжения в сечении T максимальны.
значение в точках, прилегающих к балке, и уменьшаются примерно по параболе
образуют до нуля на расстоянии x от торца балки. РИСУНОК 1.25 Эффективный фланец
ширина, B . Как средство
упрощение, а не изменение с расстоянием от сети, эффективное
можно принять ширину B равномерного напряжения.Эффективная ширина B составляет
зависит от длины пролета балки и зависит от: 1. Интервал
балок 2. Ширина
стенка балки 3. Соотношение
толщины плиты на общую глубину балки 4. Конец
состояние балки (несъемная или непрерывная) 5. Путь
в котором действует нагрузка (распределенная нагрузка или точечная нагрузка) 6.Соотношение
длины балки между точками нулевого момента до ширины стенки и
расстояние между полотнами. 1. Интервал
балок 2. Ширина
стенка балки 3. Соотношение
толщины плиты на общую глубину балки 4. Конец
состояние балки (несъемная или непрерывная) 5. 6.Соотношение
длины балки между точками нулевого момента до ширины стенки и
расстояние между полотнами. Египетский
Кодекс предписывает, что эффективная ширина фланца B секции T ,
как на рис. 1.26, следует принять ширину полотна b плюс эффективный
выступающие стороны фланца x 1
и x 2.
Таким образом, B = b + ( x 1 + х 2) ( 1.58 ) где x 1 + х 2
равно наименьшее из: ( 1,59a ) ( 1. ( 1,59c ) где L 2 —
расстояние между точками нулевых моментов. Для балки с простой опорой
расстояние L 2 указано
выше — это просто расстояние между центрами опор. Для балок
продолжается с одного конца и просто поддерживается с другого конца, расстояние L 2
можно принять за 0.80-кратное расстояние между центрами опор. За
балки сплошные с обоих концов, расстояние L 2
может быть принято равным 0,70 пролета между центрами опор. t s 1 и т с 2 — толщина правой и левой плиты
и S 1
и S 2
— чистые расстояния до следующих правого и левого лучей. РИСУНОК 1.26 Эффективная ширина фланца Т -балк. Для увеличения силы сжатия изолированного
прямоугольные балки, добавлены бетонные выступающие стороны полки, рис. и РИСУНОК 1.27 Изолированный T -образный
разделы. Торцевая балка
балочного перекрытия называют балочным перекрытием. Балка стыкуется с плитой
только с одной стороны. РИСУНОК 1.28 Эффективная ширина фланца L -балки. Египетский кодекс определяет, что эффективная ширина фланца B должна
за ширину стенки b плюс эффективная ширина выступающей полки x 1.Таким образом, B = b + x 1 ( 1,61 ) где x 1
равно наименьшее из: конструкция перевернутого L -образного профиля может примерно выполните ту же процедуру, что и для профилей T и I , но с
используя соответствующую эффективную ширину B . 1,10
Расчет на изгиб железобетонных фланцевых секций На фланцевых участках видно, что большая площадь
компрессионного фланца, образующего часть плиты, эффективно сопротивляется
большая часть или вся сила сжатия из-за изгиба. Если раздел
разработан на этой основе, глубина паутины будет небольшой; следовательно
момент рычага y ct мала, что приводит к большому количеству растянутой стали, что нежелательно. Из-за большой площади сжатия
фланец, конструкция сечения T не требует, в большинстве практических случаев,
рассмотреть дважды усиленный разрез. 1.10.1 Эффективная глубина d Во многих случаях
эффективная глубина d может быть известна на основе изгибной конструкции
сечение у опоры в неразрезной балке, e.грамм. раздел 2-2 на рис. 1.29a.
Сечение опоры подвергается действию отрицательного момента, при этом плита
при растяжении и игнорируется, а ширина балки равна ширине стенки b . РИСУНОК 1.29 Системы перекрытий и балок Iýýýf эффективная глубина d секции 1-1 дюйм
Рис. 1.29b неизвестен, приблизительную эффективную глубину можно получить с помощью
с учетом прямоугольного сечения с уменьшенной шириной
, Рис.1.30. Уменьшенная ширина
больше ширины стенки b и меньше
эффективная ширина фланца B . Разумный выбор
соотношение варьируется между
и в зависимости от приложенного момента и требований к сдвигу. ( 1.63 ) РИСУНОК 1.30 Уменьшенная ширина профиля T . Это также
можно оценить эффективную глубину d с помощью ( 1,64 ) В таблице D.1 приведены значения для K 1 мин для
все марки стали и ряд обычно используемых значений прочности бетона. 1.10.2 Конструкция T — и I — секций Как уже говорилось в разделе 1.9, конструкция профиля I аналогичен профилю T . Когда глубина эквивалента
блок напряжений и находится внутри фланца; то есть т с ,
сечение ведет себя как прямоугольное сечение с шириной балки, равной
ширина фланца. Если т с , сечение может быть выполнено в виде прямоугольного
сечение шириной В , рис. 1.31. РИСУНОК 1.31.
Поведение прямоугольного сечения. Дизайн может
можно начать с предположения, что a т с .Принимая моменты сил о натяжной стали, получаем ( 1,65 ) раствор
квадратное уравнение дает a . Если т с как
предполагается, что натяжная сталь может быть найдена с помощью ( 1.66 ) Когда глубина блока эквивалентных напряжений равна
больше толщины фланца, т.е. a > t s ,
сечение может быть спроектировано с использованием уравнений для дважды армированной балки, как
следует. Как показано на рис. 1.32, натяжная сталь A s может
считается разделенным на область A s 1,
которая сопротивляется сжатию в бетоне по стенке, и площадь A s 2
или A SF ,
который противостоит сжатию бетона при выступе фланца. РИСУНОК 1.32. Дизайн
a T — сечение при a a макс . Предполагая, что сталь растяжения поддается,
с учетом уравнения T 2 = С 2,
затем ( 1,67 ) или ( 4.68 ) Конечный момент сечения — это сумма
два момента M u 1 и M u 2: ( 1,69 ) где ( 1.70 ) и ( 1,71 ) решение квадратного уравнения дает a . Если a макс Это означает, что раздел подходит без
.Учитывая уравнение, T 1 = С 1,
затем ( 1,72 ) или ( 1,73 ) Общий объем стали, использованной в секции T , составляет ( 1. Если a > a макс Отсюда следует, что
необходимо, рис. 1.33. Здесь также ( 1,73 ) Конечный момент сечения — это сумма
три момента M u 1, M u 2 и M u 3: ( 1.75 ) где ( 1,70 ) ( 1,76 ) и ( 1,77 ) и ( 1.78 ) Общий объем стали, использованной в секции T , составляет ( 1,79 ) Если, то ( 1,80 ) РИСУНОК 1.33. Дизайн
a T — Секция, a > a макс . Решение египетского кода Египетский кодекс допускает другой подход к определению A с когда a > t s . ( 1.81 ) давая ( 1,82 ) РИСУНОК 1.34. Дизайн
a T — сечение. Пример 1.5 A T — балка
сечение с B = 1000 мм, b = 250 мм и t s =
100 мм должна иметь расчетную прочность на изгиб M u 450 кНм.Если f cu =
25 Н / мм2 и
сталь 360/520, рассчитайте требуемую площадь стали, если: а. d = 550 мм б. d = 440 мм c. d = 400 мм РИСУНОК 1.35. Пример 1.5. Решение: Предположим, a т с . дача: Деталь a : d = 550 мм раствор
квадратное уравнение дает = 79 мм, что меньше t s .
Таким образом, секция будет вести себя как прямоугольная секция. Для равновесия, C = T , имеем A с =
2818 мм2;
используйте 6 25. мм2;
использовать 3 12. Деталь b: d = 440 мм раствор
квадратное уравнение дает = 104 мм, что больше t s .
Следовательно, требуется конструкция сечением T . Со ссылкой на рис. 1.32,
для равновесия, следовательно, от у нас кНм давая кНм Решение квадратного уравнения дает a = 116 мм
и c = 145 мм. Но c макс =
0,44 d = 0,44 x
440 = 193,6 мм, что больше c . Для равновесия T = C 1 + С 2,
отсюда с кН у нас дает A с =
3710 мм2 Другое решение Для равновесия C 1 = Т 1,
мы можем поставить что дает A s 1 =
1034 мм2 Также для равновесия C 2 = Т 2,
мы можем поставить A SF = A s2 = 2675 мм2 A с = А s1 + A s2 = А s1 + A SF =
1034 + 2675 = 3709 мм2 A s1 = А с — A SF =
1034 мм2
что меньше A smax = кв. и больше A smin = м мин б
г = х
250 х
440 = 336.11 мм2 Решение египетского кода Если пренебречь сжатием в веб-части ниже
нейтральная ось, имеем мм2 Деталь c: d = 400 мм решение квадратного уравнения дает a =
118,5 мм, что больше t s .Следовательно, требуется конструкция сечением T . Для равновесия
, следовательно из кН у нас кНм давая кНм Решение квадратного уравнения дает a = 182 мм
и c = 227,5 мм. Но c макс =
0.44 d = 0,44 х
400 = 176 мм, что меньше c . Это означает, что компрессионная сталь
требуется, рис. 1.33. Здесь также кНм A SF = A с 2 =
2675 мм2 a макс =
0,80 c макс =
140 мм кНм A s1 = A smax =
м макс б
d = 5 х
10-4 х
25 х
250 х
400 = 1250 мм2 кНм Так как меньше 0. = 255,56 мм2 A с = А s1 + А s2 + A s3 = A smax + А SF +
= 1250 + 2675 + 255,56 = 4180.6 мм2 Решение египетского кода Если пренебречь сжатием в веб-части ниже
нейтральная ось, имеем = 0,10 A с =
410,7 мм2 или
более. Пример 1.6 В перекрытии-балке
система перекрытий, наименьшая эффективная ширина фланца B оказалась равной 1450
мм, ширина полотна b составляла 250 мм, а толщина плиты составляла 120 мм, рис.
1.36a. Спроектируйте сечение T для противодействия предельному внешнему моменту M u 240 кНм. РИСУНОК 1.36. Пример
1.6. Решение: Поскольку эффективная глубина не указана, уменьшенное
ширина фланца принята; сказать . Таким образом, мм. То есть эквивалентное прямоугольное сечение, рис. 1.36b,
можно выбрать с помощью B r =
580 мм и что дает d = 380 мм. Предположим, что два ряда
стальные стержни (будут проверены позже). т = 380,8 + 75 = 455,8 мм; скажем, т = 500
мм фактическая d = 500 — 75 = 425 мм Выполните, как в предыдущем примере, чтобы вычислить A s . Предположим, a т с a = 46 мм, что меньше t s Для равновесия T = C , мы
иметь мм2 выбрать
6 ж
25 (2950 мм2) не должно быть меньше 0. РИСУНОК 1.37. Пример
1.6. 1.11 Конструкция секций T и I с использованием средств проектирования Если известны b и d ,
конструкция профиля T имитирует прямоугольное сечение, когда , с b равно B , рис.1.38a. В противном случае, если a > как на рис. 1.38b, код позволяет не учитывать
сжатие в перегородке под фланцем, как показано на рис. 1.38c. Сначала рассчитайте соотношение
и K 1
с ( 1,67 ) Тогда при известном значении
, определите соответствующую таблицу параметров (Таблицы E.1
через E.5). Двигайтесь вертикально к
ценность, а также
значение, затем по горизонтали до K 1
значение, и, наконец, получить значение K 2 до
использоваться. Затем вычислите A s с ( 1,68 ) Если a >
принимают значение K 2 , что
соответствуют a =. РИСУНОК 1.38. Конструкция Т и I разделы Пример 1.7: В перекрытии-балке
система перекрытий, наименьшая эффективная ширина фланца B оказалась равной 1450
мм, ширина полотна b составляла 250 мм, а толщина плиты составляла 120 мм. Дизайн
a T — сечение для сопротивления предельному внешнему моменту M u из
240 кНм.Дано: f cu =
20 Н / мм2 и
сталь 240/350. Решение: =
580 мм =
380 мм Предположим, что два ряда стальных стержней (до
будет проверено позже) т = 380 + 75 = 455 мм; сказать t = 500 мм и, следовательно, фактический d = 500-75 = 425 мм =, Что дает K 1 =
1.0446 Введите
Таблица E.1 и получаем K2 =
197,3 и a = 0,40 t s =
48 мм. 2862 мм2
(Используйте 6 f
25) и = 286,2 мм2
(Используйте 3 f
12) Пример 1.8: A T — секция балки с B = 1000 мм, b = 250 мм и t s =
100 мм должна иметь расчетную прочность на изгиб M u 450 кНм.Использование f cu =
25 Н / мм2 и
сталь 360/520, рассчитайте требуемую площадь стали, если d = 550, 440 и
400 мм. Решение: а. d = 550 мм =, Что дает K 1 =
0,8198 Войдите в таблицу E.3 и получите К 2 =
291,2 и a = 0,80 t s =
80 мм.Затем = 2810 мм2
(Используйте 6 25)
и = 281 мм2
(Используйте 3 12) б. d = 440 мм =, Что дает K 1 =
0,6558 Введите
Таблица E.3, начиная с a > t s ,
возьмем K 2 =
277,8 при a = t s . = 3682 мм2
и = 368,2 мм2 c. d = 400 мм =, Что дает K 1 =
0,596 Введите
Таблица E.3, начиная с a > t s ,
возьмем K 2 =
273,9 при a = t s .
Затем = 4107 мм2
и = 410.7 мм2 Назад
Вверх Раздел Рисунок 7.9 Балка с двойным усилением для противодействия заклиниванию 1. В качестве коэффициента уменьшения момента 6 = 0,80. предельная глубина нейтральной оси x = {6- QA) d = (0,8-0,4) x 540 = 216 мм 2. K M / bd% = 370 x 106 / (300 x 5402 x 25) 3. Х, | = 0,454 (A «- 0,4) — 0,182 (5 — 0,4) 2 = 0. Из пропорций диаграммы деформации 0,0035 (.v — d ‘) Деформация стали при сжатии eK = —— 0,0035 (216-100) 216 Напряжение сжатия стали = EteK _ (0,169 — 0,152) 25 x 300 x 5402 376 (540-100) Предусмотрите две планки h30 для площади 628 мм2, дно из стали. 5. Сталь натяжная 0,87 / ykZ s0,87 / yit, где z = d- () .a «r / 2 = 540 — 0,8 x 216/2 = 454 мм, следовательно, 0,152 x 25 x 300 x 5402376 a = __ l x_ 0.S.req) — (As.prov — ASircq) То есть 628 — 224 (= 404)> I960 — 1877 (= 83) мм2 7. Эти области лежат в максимальных и минимальных пределах, указанных в коде. Чтобы ограничить сжатие стали, звенья диаметром не менее 8 мм на расстоянии 300 мм должны быть Я предоставил. Рисунок. 7.10 показаны сечения тавровой балки и двутавровой балки, которые составляют часть. бетонное перекрытие и перекрытие с перекрытием перекрытия между балками и площадками.Предполагается, что имеется трещина, поэтому балка должна иметь прямоугольное сечение шириной /> «и общей глубиной h. На промежуточных опорах неразрезных балок, где возникают заклинивающие моменты th. общая площадь растянутой арматуры должна быть распределена по полезной ширине фланца, как показано на рисунке 7. Эффективное отклонение ширины фланца определяется следующим уравнением: ¿> ошибся.i = 0,2bt + 0,1 / n <0,2 / (), а также быть (ft \ 2b, — это расстояние в свету между перемычками соседних балок / o — это расстояние между точками обратного прогиба вдоль балки, как показано на рисунке 7.11. Рисунок 7.10 Тавровая балка и двутавровая балка Поперечная втулка во фланце Раздел Раздел Рисунок 7.11 Размеры, которые будут использоваться при расчете эффективной ширины фланца b, ii b, ii Продолжите чтение здесь: Информация Была ли эта статья полезной? Документ конференции В статье анализируется эффективность метода приповерхностного монтажа (NSM) из армированных волокном полимеров (FRP) для упрочнения на сдвиг железобетонных балок. Эти ключевые слова были добавлены машиной, а не авторами. Этот процесс является экспериментальным, и ключевые слова могут обновляться по мере улучшения алгоритма обучения. Это предварительный просмотр содержимого подписки, , чтобы проверить доступ. Невозможно отобразить предварительный просмотр. Скачать превью PDF. De Lorenzis, L.& Нанни, А. 2001. Усиление сдвига железобетонных балок с помощью полимерных стержней, армированных волокном, приповерхностных. 98 (1): 60–68. Dias, S J.E. & Barros, J.A.O. 2008. Усиление на сдвиг железобетонных балок Т-образного сечения методом приповерхностного монтажа. 12 (3): 300–311. Dias, S.J.E. И Баррос Дж. А.О. 2010. Характеристики железобетонных тавровых балок, усиленных на сдвиг с помощью NSM CFRP. 32 (2): 373–384. Dias, S.J.E., Bianco, V. Barros, J.A.O. & Монти, Г. 2007. Ж / б балки с Т-образным поперечным сечением малой прочности, усиленные сдвигом методом NSM.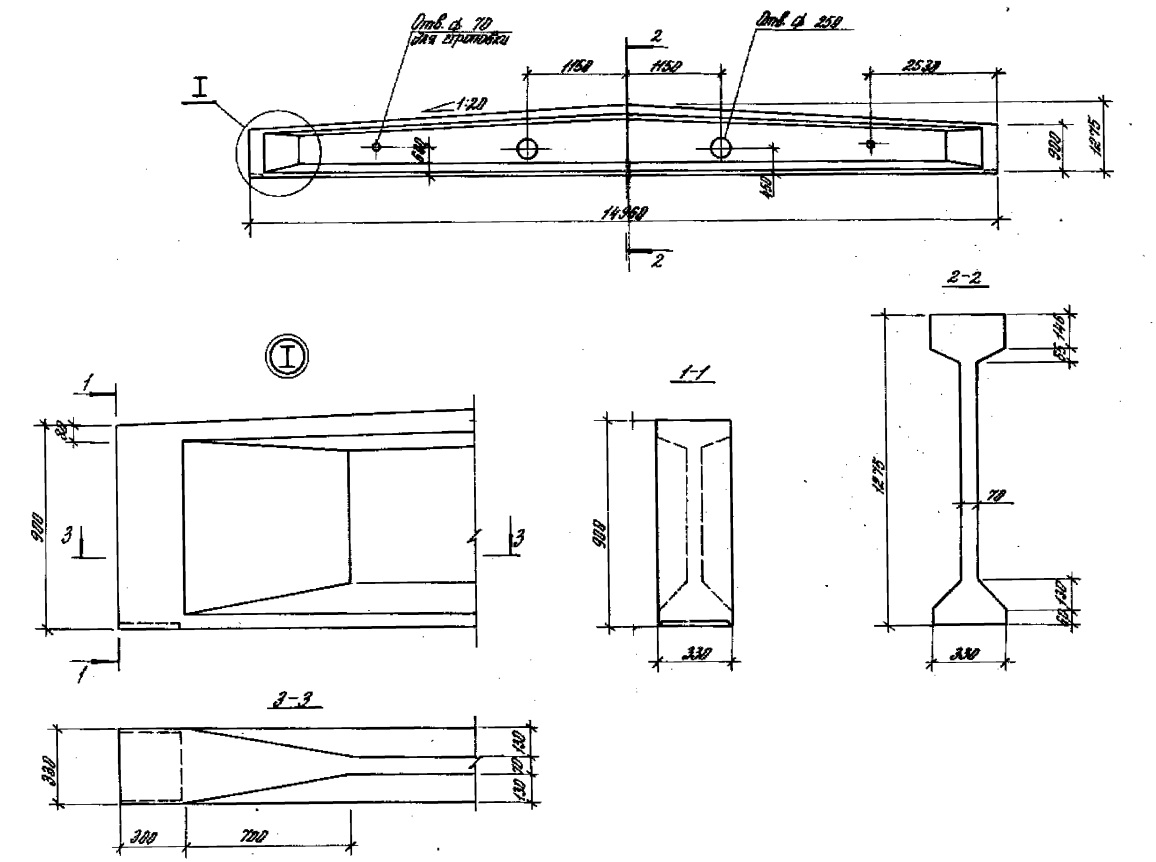 5 * диаметр продольной стали Уравнение 7
5 * диаметр продольной стали Уравнение 7 Пример:
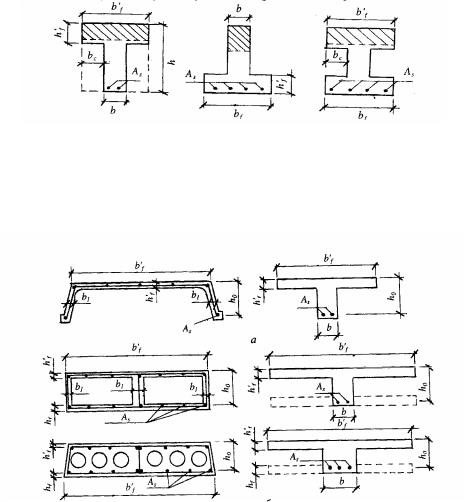 Какова площадь растянутой стали в середине пролета, чтобы выдержать факторный момент 725 кН.м? Свойства материала: fc ’= 21 МПа и fy = 420 МПа.
Какова площадь растянутой стали в середине пролета, чтобы выдержать факторный момент 725 кН.м? Свойства материала: fc ’= 21 МПа и fy = 420 МПа. Решение:

Часто задаваемые вопросы
Что такое Т-балка железобетонная?  Балка называется Т-образной.
Балка называется Т-образной. Страница не найдена для балок 2_internal_t
 *
* Страница не найдена для t beam_versus_rectangular_beam
 *
* Страница не найдена для конструкции_армированной_бетонной_т балки
 *
* Основные понятия, прямоугольные балки и тавровые балки
Основные понятия, прямоугольные балки и тавровые балки
 1.19а,
1.19а, ( 1,56 ) ( 1,57 ) 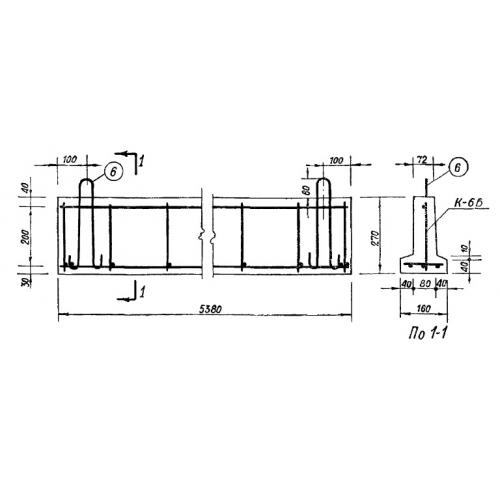
150 кНм. 414 мм мм2 6 ж 20 4 ф 25 1960 5 ж 22 1960 9 ж 16 1800 2 ж 25 + 2
f 22 1740  Если 2
ж
Выбрано 25 плюс 2 f 22, A s =
1740 мм2,
что на 102 мм2 меньше
чем требуемая площадь 1842 мм2.
Но поскольку габаритная глубина т может быть увеличена на долю 50 мм,
фактическая эффективная глубина будет немного больше расчетной d min ,
следовательно, уменьшая требуемую A s .
Если 2
ж
Выбрано 25 плюс 2 f 22, A s =
1740 мм2,
что на 102 мм2 меньше
чем требуемая площадь 1842 мм2.
Но поскольку габаритная глубина т может быть увеличена на долю 50 мм,
фактическая эффективная глубина будет немного больше расчетной d min ,
следовательно, уменьшая требуемую A s . Из-за небольшого разброса
уменьшение требуемой площади стали можно приблизительно представить соотношением
вычислено d к фактическому d . А с на самом деле нужно:
Из-за небольшого разброса
уменьшение требуемой площади стали можно приблизительно представить соотношением
вычислено d к фактическому d . А с на самом деле нужно: 1693 мм2 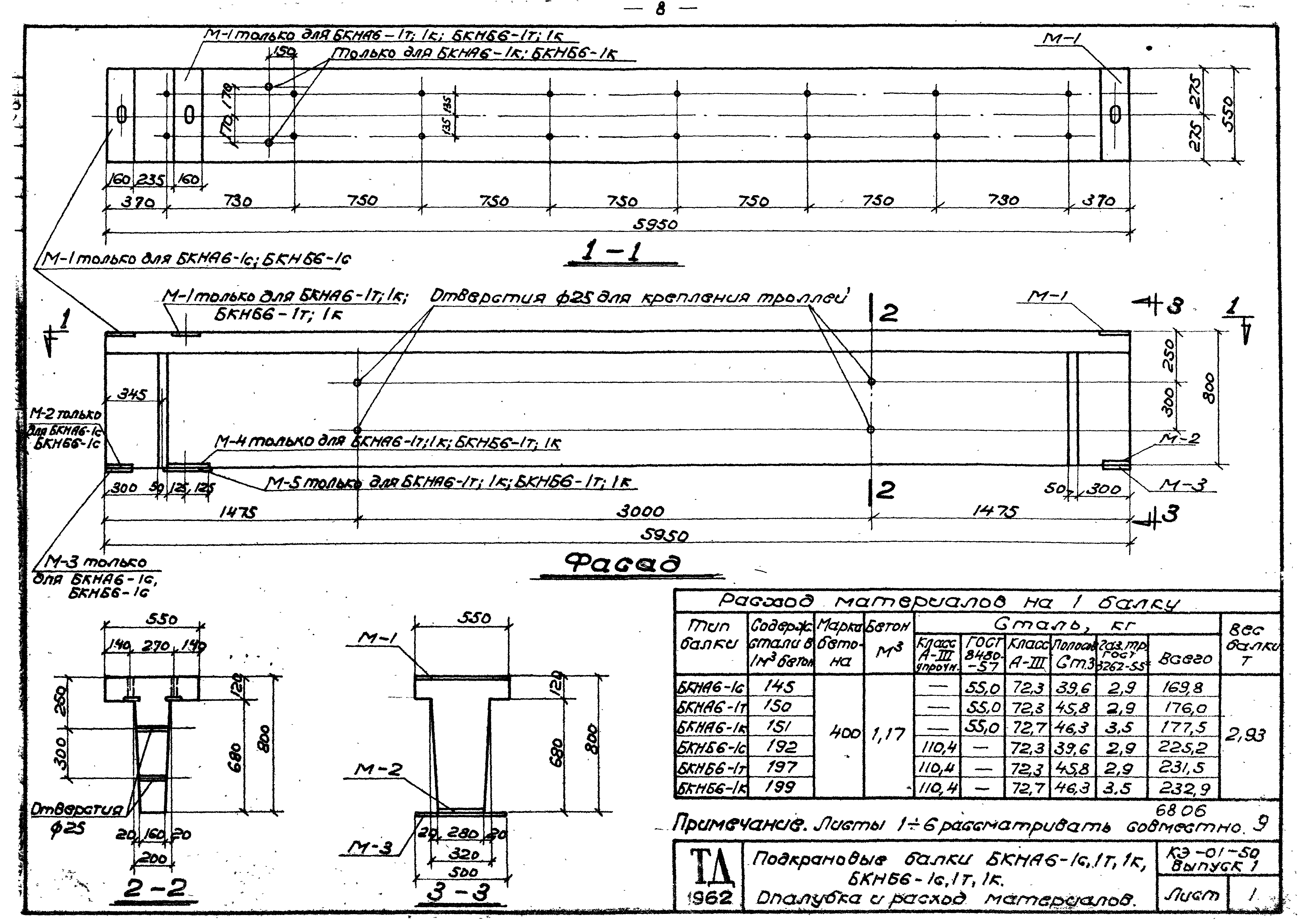 Общая глубина т. составляет, таким образом,
Общая глубина т. составляет, таким образом, К 2 =
208. Затем, 1630 мм2
(Используйте 3
ж
22 + 3
ж
19) 442 мм2 мм2  3 = 1,3
1630 = 2119 мм2
3 = 1,3
1630 = 2119 мм2 мм2 что дает K 1 =
0.468. 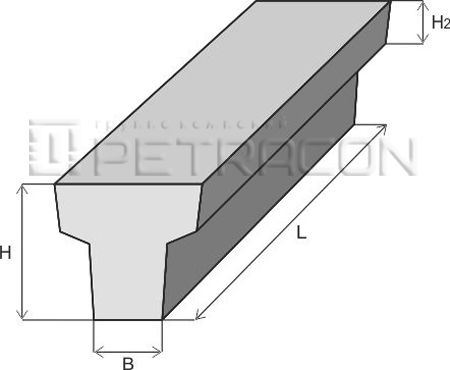 Отсюда следует, что необходимо. Войдите в Таблицу C.3 (где 0,10) и получаем K 2 =
201,8 и
= 0,225.
Отсюда следует, что необходимо. Войдите в Таблицу C.3 (где 0,10) и получаем K 2 =
201,8 и
= 0,225. 1416 мм2 319 мм2 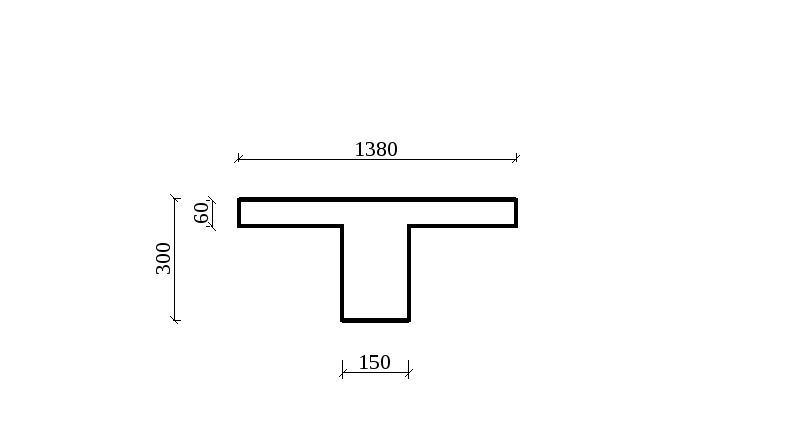 1.23.
1.23. Подчеркивает также
варьироваться по вертикали от максимума на верхних волокнах фланца до минимума на
нижние волокна фланца.
Подчеркивает также
варьироваться по вертикали от максимума на верхних волокнах фланца до минимума на
нижние волокна фланца. Путь
в котором действует нагрузка (распределенная нагрузка или точечная нагрузка)
Путь
в котором действует нагрузка (распределенная нагрузка или точечная нагрузка) или при t s 1 = т с2 _27.png) 59b )
59b ) 1.27. Этот
изолированный T -образный профиль чаще всего используется в качестве сборных элементов.
Египетский кодекс определяет размер отдельных секций T как:
1.27. Этот
изолированный T -образный профиль чаще всего используется в качестве сборных элементов.
Египетский кодекс определяет размер отдельных секций T как: ( 1.60 ) ( 1. 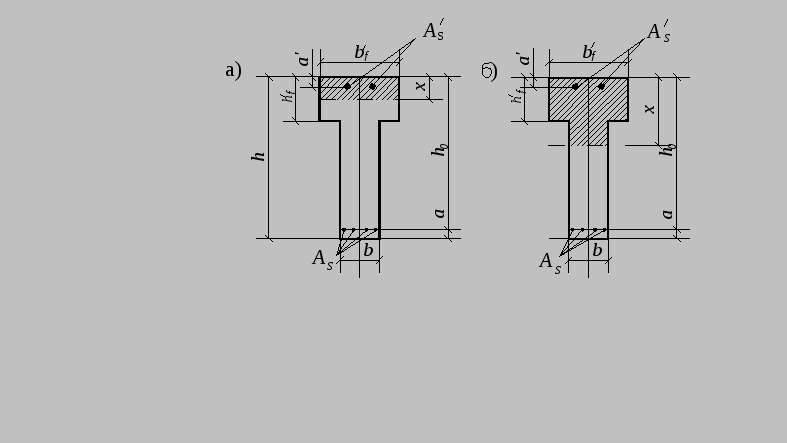 62a )
62a ) ( 1.62b ) ( 1.62c ) 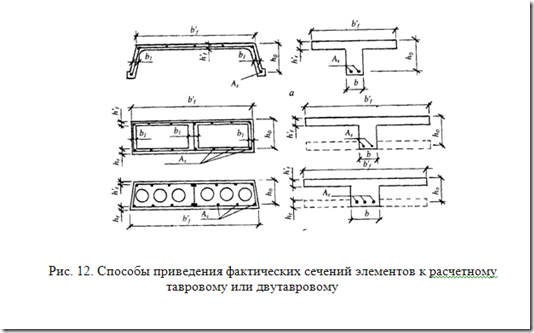 Но в случае сборных элементов, когда
ширина фланца мала, а эффективная глубина ограничена, сжатие
можно добавить сталь.
Но в случае сборных элементов, когда
ширина фланца мала, а эффективная глубина ограничена, сжатие
можно добавить сталь. Если
сдвиг большой или требуется небольшое количество, нужна большая глубина; т.е.
подходы. Для неглубоких участков используется более высокое соотношение; то есть соотношение
может подойти. После определения соотношения
, следующим шагом будет оценка эффективной глубины с помощью
уравнение
Если
сдвиг большой или требуется небольшое количество, нужна большая глубина; т.е.
подходы. Для неглубоких участков используется более высокое соотношение; то есть соотношение
может подойти. После определения соотношения
, следующим шагом будет оценка эффективной глубины с помощью
уравнение В противном случае, если больше t s ,
обязательна конструкция сечений T .
В противном случае, если больше t s ,
обязательна конструкция сечений T .
 74 )
74 )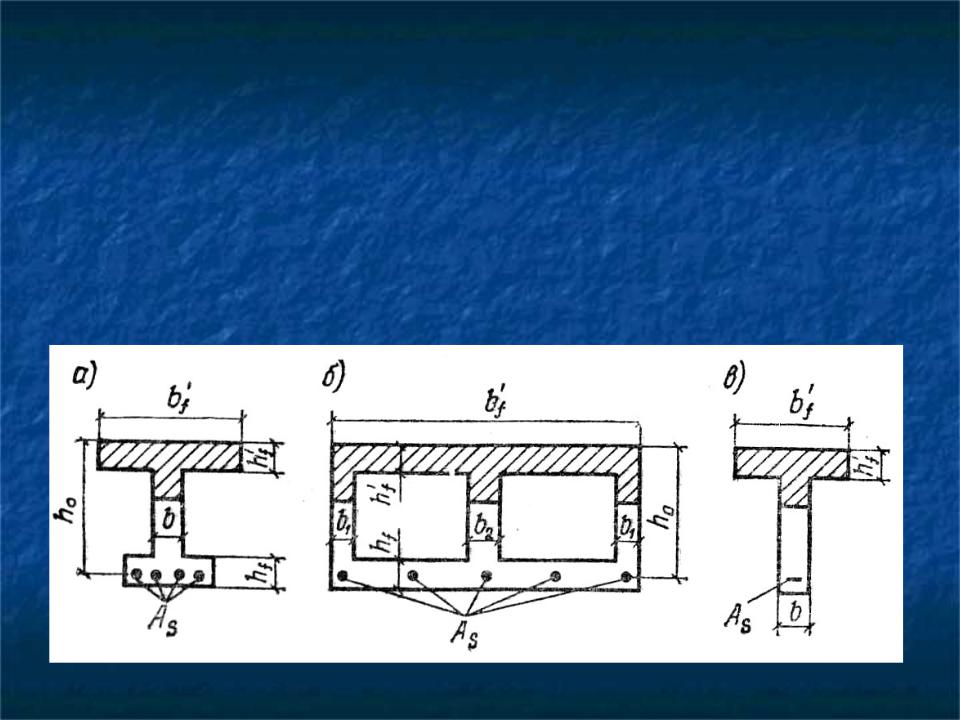 Игнорируя сжатие в перегородке под фланцем, как показано на рис. 1.34,
натяжная сталь может быть получена из:
Игнорируя сжатие в перегородке под фланцем, как показано на рис. 1.34,
натяжная сталь может быть получена из: Затем
Затем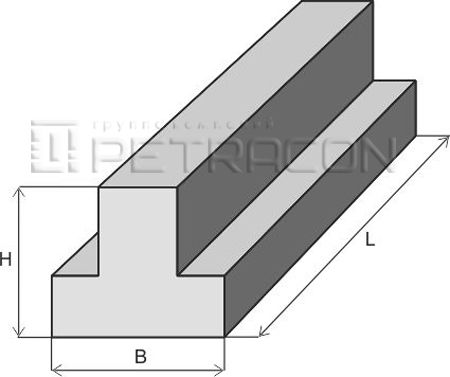 Это означает, что
раздел адекватный без.
Это означает, что
раздел адекватный без. м. макс б
d = 5 х
10-4 х
25 х
250 х
440 = 1375 мм2
м. макс б
d = 5 х
10-4 х
25 х
250 х
440 = 1375 мм2 15 для стали 360/520, это означает, что
.
15 для стали 360/520, это означает, что
. мм2  Дано: f cu =
20 Н / мм2 и
сталь 240/350.
Дано: f cu =
20 Н / мм2 и
сталь 240/350. 10 А с ,
используйте 3 f
12.
10 А с ,
используйте 3 f
12.
 Затем
Затем Затем
Затем т — бетонная конструкция

7,4 Балка с фланцем
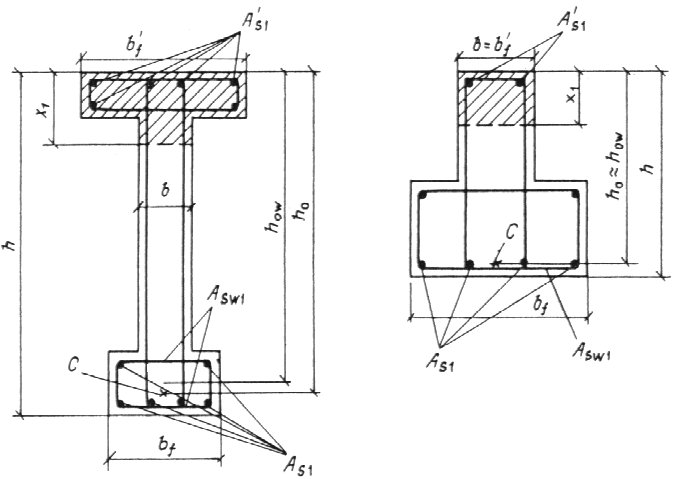 10. Часть армирования может быть сосредоточена над th. ширина полотна.
10. Часть армирования может быть сосредоточена над th. ширина полотна. Эффективность упрочнения на сдвиг Т-образных балок с армированием из стеклопластика NSM
Реферат
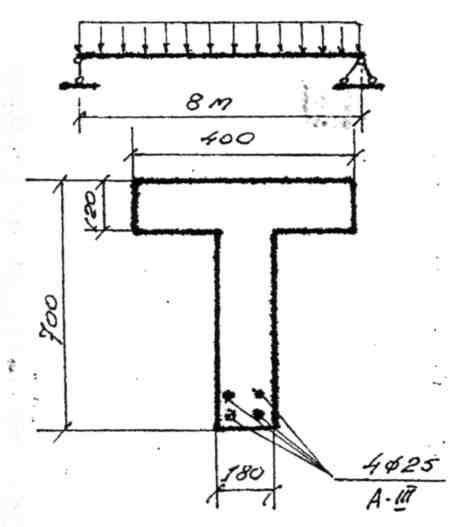 Обзор существующих исследований показывает, что количество экспериментальных испытаний и инженерной практики в этой области крайне ограничено. Однако первые результаты были многообещающими и вызвали интерес мирового сообщества FRP. Основываясь на опубликованных результатах испытаний, в документе проводится сравнительное исследование режимов разрушения, эффективности деформации FRP и повышения прочности на сдвиг. Эффективность сдвигового упрочнения NSM обсуждается в аспекте следующих параметров: форма поперечного сечения балки, размеры балки, процентное соотношение внутренней стальной арматуры, тип, поперечное сечение, наклон и шаг арматуры NSM FRP вдоль балки. ось и прочность бетона.
Обзор существующих исследований показывает, что количество экспериментальных испытаний и инженерной практики в этой области крайне ограничено. Однако первые результаты были многообещающими и вызвали интерес мирового сообщества FRP. Основываясь на опубликованных результатах испытаний, в документе проводится сравнительное исследование режимов разрушения, эффективности деформации FRP и повышения прочности на сдвиг. Эффективность сдвигового упрочнения NSM обсуждается в аспекте следующих параметров: форма поперечного сечения балки, размеры балки, процентное соотношение внутренней стальной арматуры, тип, поперечное сечение, наклон и шаг арматуры NSM FRP вдоль балки. ось и прочность бетона. Ключевые слова
Прочность на сдвиг, армированный бетон, армированный волокном, полимерный бетон, прочность, железобетонная балка
Предварительный просмотр
Ссылки



 М. Шапиро, А.В. Агарков // Строительная механика инженерных конструкций и сооружений.- 2007. — № 1. — С. 39 – 47.
М. Шапиро, А.В. Агарков // Строительная механика инженерных конструкций и сооружений.- 2007. — № 1. — С. 39 – 47. 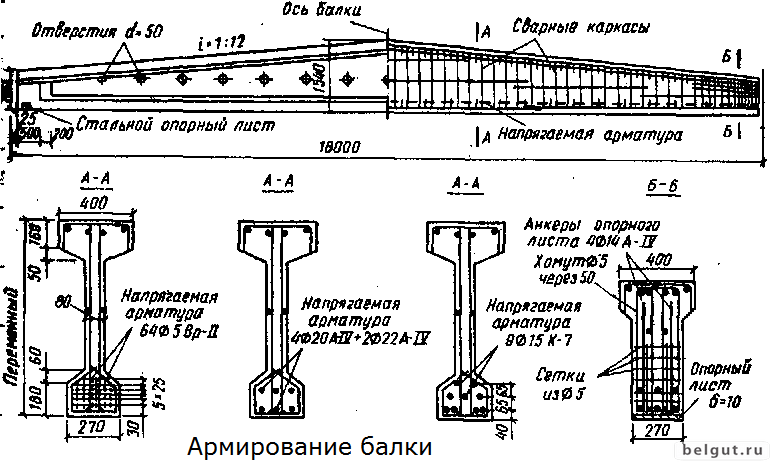
 Кроме того зазор между балками можно предварительно заполнить цементным раствором и забить в него пластину, для чего одна грань последней скошена.
Кроме того зазор между балками можно предварительно заполнить цементным раствором и забить в него пластину, для чего одна грань последней скошена.