Арматурный калькулятор: Калькулятор веса арматуры. Вес метра арматуры. Количество метров арматуры в тонне.
Арматурный калькулятор (2 в 1)
, 03 мая 2007 в 21:15#1
ништяк проги, спасибо =)
abpost , 05 мая 2007 в 21:54#2
Установка слоя, цвета, типа и веса линии, масштаба линии, стиля текста, размерного стиля, масштаба размера, свойств штриховки в ЛЮБОЙ комбинации (задается) есть в программе VetCAD++. Всем рекомендую — давно пользуюсь и сейчас без нее как без рук.
abpost , 05 мая 2007 в 21:56#3
Также в ней есть возможность заполнять спецификации, формировать автоматически ведомости расхода стали (и арматура, и прокат), вносить свои изделия в базу, база готовых типовых изделий и многое другое. Кто работает с монолитом, тот поймет.
Сименс , 18 мая 2007 в 00:22#4
Спасибо, где вы были раньше когда я курсач делал, а веткадом пользуюсь — доволен
#5
Спасибо. Прога хорошая и удобная. Правда на моем компе кнопка копировать не работает, на соседском — всё нормуль. Хотелось бы объединения двух прог в одну и неограниченное 10-тью количество стержней при подсчете массы арматуры. В целом прога удобная пользуюсь уже месяц. Очень доволен.
Прога хорошая и удобная. Правда на моем компе кнопка копировать не работает, на соседском — всё нормуль. Хотелось бы объединения двух прог в одну и неограниченное 10-тью количество стержней при подсчете массы арматуры. В целом прога удобная пользуюсь уже месяц. Очень доволен.
#6
Программы отличные. Вот только в проге подсчета массы стержней пропущен 30 диаметр.
Стажер , 12 ноября 2008 в 08:00Хорошее подспорье молодым. Спасибо большое!
EvgeniusZ , 16 декабря 2013 в 13:38#8
Благодарю. Количество стержней и длина вводится произвольные 🙂
elena ctenich , 28 августа 2020 в 19:20#9
Спасибо, Andy , очень удобный калькулятор. А Вы можете его немного доработать?
1. Сделать так, чтобы в окне были видны сразу все диаметры, без прокрутки (ещё An_at просил добавить диаметр 30), из-за этого немного увеличится высота окошка.
Сделать так, чтобы в окне были видны сразу все диаметры, без прокрутки (ещё An_at просил добавить диаметр 30), из-за этого немного увеличится высота окошка.
3. Слово ДЛИНА с одной Н, а то немного напрягает…
Заранее спасибо…
Калькулятор металлопроката онлайн — Metsi.ru
Если Вам нужно узнать вес погонного метра трубы, арматуры или другого проката, то наиболее удобным и простым решением является наш калькулятор металла.
Сначала Вы выбираете номенклатуру, по которой хотите произвести расчет метров в тонны.
Далее Вы выбираете размер продукции.
Для удобства использования калькулятора мы разработали интерактивную строку поиска, которая облегчит выбор размера продукции
Если это круглый прокат, то в списке представлены диаметры (арматура 10,12 и т.д., круг).
В случае если Вы хотите узнать вес трубы, то обратите внимание на толщину стенки.
Чтобы узнать вес листа, нужно выбрать толщину, и далее расчет массы будет происходить на квадратные метры.
Затем в одно из полей вносятся данные в метрах или тоннах
Если Вы будете вводить значения в поле «метры» («кв. метры», чтобы узнать вес листа), тогда вы узнаете общую массу всей длины (например, вес арматуры).
В случае если Вас интересует расчет длины по массе, то ввод данных нужно производить в поле «тонны».
Вы можете записать и распечатать полученные результаты
Наш калькулятор позволяет записывать полученные расчеты в специальном поле, чтобы Вы легко могли видеть свои последние вычисления. Для этого Вам необходимо нажать на кнопку «Записать», и в специальном поле появится результат Ваших расчетов.
Также, после того как Вы рассчитали все необходимые данные, можно нажать на кнопку «Печать» и в удобной форме получить распечатку полученных результатов.
Расчет заявки онлайн
Вы можете сравнить цены на выбранные позиции у всех поставщиков.
Для этого нужно записать Ваши вычисления. Обратите внимание, чтобы в поле с записанными результатами были позиции, которые Вам интересны. Далее, нажимаете «Рассчитать всю заявку онлайн», и система переведет Вас на страницу, где будут показаны результаты обработки цен поставщиков.
Арматурные каркасы — ООО «АВ-Сервис»
Калькулятор арматуры
Калькулятор арматурных каркасов
Арматурный каркас — металлоконструкция, которая сегодня широко используются в строительстве промышленных и гражданских объектов. Изготовленная из проволоки или арматурного прута конструкция позволяет сократить сроки строительства, повысить прочность и устойчивость возводимых сооружений к динамическим нагрузкам.
Виды арматурных каркасов
Арматурные каркасы выпускаются по ГОСТ 10922-90, устанавливающему общие технические требования к производству сварных арматурных изделий для ж/б конструкций. Согласно указанному стандарту, выпускаются каркасы двух видов:
- плоские;
- пространственные (объемные).

Плоские каркасы получают из продольных и поперечных стержней из арматурной стали, соединенных в местах их пересечений сваркой. В каркасах этого вида все стержни одного направления размещены в одной плоскости. Такие каркасы применяются для армирования железобетонных изделий и конструкций малой толщины. Их можно использовать при закладке плитного фундамента или для формирования армопояса в малом жилищном строительстве.
В пространственных каркасах стержни располагаются в разных плоскостях. Форма сечения у объемных каркасов может быть разной:
- прямоугольной;
- круглой;
- криволинейной;
- переменной по длине каркаса.
Пространственные каркасы из-за своего разнообразия имеют гораздо более широкую сферу применения. В строительстве домов, например, пространственные каркасы применяют при заливке ленточного фундамента.
Стержни каркасов выполняются из низколегированной или углеродистой стали.
Преимущества применения конструкций
Применение арматурных каркасов, изготовленных из прочной стали, увеличивает срок эксплуатации железобетонных конструкций, минимизирует риск появления трещин и прогибов. Применение арматурных каркасов позволяет:
- сократить производственный/строительный цикл;
- снизить себестоимость строительных работ без снижения прочностных характеристик сооружения.
В нашей компании вы можете купить арматурные каркасы нужных размеров и заданной конфигурации из прута или проволоки. Вся продукция изготовлена методом сварки из материалов, отвечающих требованиям соответствующих СНиП. Предлагаемые каркасы подходят для бетонных работ всех видов. Перед тем как купить нужный каркас, можно произвести расчет всех его параметров с помощью калькулятора на сайте.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}} LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Вес арматуры стальной рифленой А3
Таблица расчета веса арматуры стальной рифленой А3
В соответствии с требованиями
ГОСТ 5781-82.
• АРМАТУРУ РИФЛЕНУЮ А3 • АРМАТУРУ ГЛАДКУЮ А1 • АРМАТУРУ КОМПОЗИТНУЮ Первый поставщик арматуры. Низкие оптовые и розничные цены. Консультация по выбору. Оформление заказа на сайте и в офисе. Нарезка в размер. Доставка по Беларуси, в том числе, и в выходные дни. |
Теоретический вес, удельный вес 1 метра погонного стальной рифленой арматура А3 (А500С / S500)
| Диаметр арматуры, мм | Вес 1 метра погонного арматуры, кг | Количество метров арматуры в 1 тонне | Площадь поперечного сечения арматуры, см2 |
| 6 | 0,222 | 4504,5 | 0,283 |
| 8 | 0,395 | 2531,65 | 0,503 |
| 10 | 0,617 | 1620,75 | 0,785 |
| 12 | 0,888 | 1126,13 | 1,131 |
| 14 | 1,21 | 826,45 | 1,54 |
| 16 | 1,58 | 632,91 | 2,01 |
| 18 | 2 | 500 | 2,54 |
| 20 | 2,47 | 404,86 | 3,14 |
| 22 | 2,98 | 335,57 | 3,8 |
| 25 | 3,85 | 259,74 | 4,91 |
| 28 | 4,83 | 207,04 | 6,16 |
| 32 | 6,31 | 158,48 | 8,04 |
| 36 | 7,99 | 125,16 | 10,18 |
| 40 | 9,87 | 101,32 | 12,57 |
| 45 | 12,48 | 80,13 | 15 |
| 50 | 15,41 | 64,89 | 19,63 |
| 55 | 18,65 | 53,62 | 23,76 |
| 60 | 22,19 | 45,07 | 28,27 |
| 70 | 30,21 | 33,1 | 38,48 |
| 80 | 39,46 | 25,34 | 50,27 |
Смотрите также: Online-калькулятор расчета веса и длинны стальной арматуры А3 в зависимости от диаметра.
Сколько весит стальная рифленая арматура А3 А500С / S500? Как рассчитать вес арматуры? Как перевести метры погонные в килограммы и тонны? Ответы на эти вопросы вы найдете в приведенной выше таблице расчета веса арматуры в зависимости от диаметра. Масса арматуры, теоретический удельный вес 1 метра погонного арматуры, количество метров арматуры в 1 тонне.
На сайте металлобазы «Аксвил» вы можете купить арматуру в Минске оптом и в розницу.
Смотрите также: Металлопрокат по размерам и типам.
Узнайте как определить Вес арматурной сетки + калькулятор!
Вес арматурной сеткиБетонная отливка, используемая для создания фундаментных оснований сама по себе является довольно прочной конструкцией. Однако прочность ее велика только в одном направлении – а именно бетон хорошо сопротивляется давлению.
Но на бетонные основания могут воздействовать и нагрузки по другим направлениям. Например, она может испытывать влияние на изгиб, скручивание и так далее. Грунт является неоднородной субстанцией и при замерзании может изменять свою структуру и объем, расширяясь в разных направлениях.
Для того, чтобы придать бетонной отливке прочность и устойчивость к воздействию по любым направлениям – в тело бетонной отливки внедряется металлический силовой каркас.
Металлический каркас в бетонных отливках применяется не только при строительстве фундаментов. Он также создается и при других бетонных работах, например, при строительстве лестниц или при создании выравнивающей цементно-песчаной стяжки.
Металлический каркас бетонной отливки может создаваться различными способами. Так, пространственный каркас может создаваться из металлических прутков, которые связываются между собой в местах пересечений. Фиксироваться прутья могут вязальной проволокой, хомутами или электросваркой.
Отличным решением при формировании металлического каркаса может стать использование арматурной сетки.
Арматурная сетка. Характеристики и примеры использования
Арматурная сетка формируется из металлической проволоки или из арматурных прутьев большего сечения в промышленном производстве. Этим достигается точность размеров шага сетки, что положительно сказывается на общем качестве железобетонной конструкции.
Этим достигается точность размеров шага сетки, что положительно сказывается на общем качестве железобетонной конструкции.
В процессе ее изготовления отрезки проволоки или арматурные прутки раскладываются с определенным шагом, а затем в местах пересечения фиксируются точечной электрической сваркой.
Арматурная сетка широкой применяет в строительной отрасли, как для наружных и фундаментных работ, так и для внутренних интерьерных работ. Уложенная в несколько горизонтальных слоев в фундаменте и соединенная вертикальными перемычками – арматурная сетка становится прекрасным силовым каркасом для железобетонной отливки. Арматурная сетка, уложенная в один слой на поверхность перекрытия сможет стать основой для стяжки пола или для крепления системы теплых полов с жидким теплоносителем. Кроме того, с использованием арматурной сетки можно формировать и сложные прочные железобетонные конструкции, например, входные лестницы.
Арматурная сетка — фотоТипы арматурных сеток
Произвести классификацию арматурных сеток можно произвести по нескольким параметрам. Прежде всего, разделить на типы арматурную сетку можно исходя из толщины используемого исходного материала:
Прежде всего, разделить на типы арматурную сетку можно исходя из толщины используемого исходного материала:
- Если арматурная сетка изготавливается из сравнительно тонкой металлической проволоки – то она условной называется «тонкой»,
- В том случае, если арматурная сетка изготавливается из толстого металлического прутка, то ее можно условно назвать «толстой».
Кроме того, арматурная сетка может изготавливаться с различной степенью точности.
Может выделяться обыкновенная точность сварки, вполне пригодная для проведения наружных строительных работ и арматурная сетка с повышенной точностью. Точность сварки элементов арматурной сетки обозначается цифрами после буквы «П» в маркировке.
Образец арматурной сеткиОтдельно стоит сказать и о том, в каком виде поставляется арматурная сетка с промышленных предприятий. В зависимости от толщины используемых элементов с завод сетка может поставляться в виде плоских пластин или в виде рулонов.
Кроме того, в зависимости от назначения – арматурная сетка может изготавливаться с различной конфигурацией ячеек. Они могут прямоугольными или квадратными.
Они могут прямоугольными или квадратными.
Особенности применения арматурной сетки
Арматурная сетка может существенно сократить время на проведение строительных работ с использованием бетонных отливок.
При классическом способе формирования силового каркаса он создается из отдельных металлических прутьев. При этом создание пространственного каркаса представляется довольно сложным занятием. Каждое место пересечения арматурных прутков должно скрепляться.
Фиксация мест пересечения арматурных прутьев может производиться при помощи петель из вязальной проволоки. Она складывается вдвое, оборачивается вокруг места пересечения и закручивается с помощью заостренного крюка или специальными автоматическими устройствами.
Естественно такая фиксация может занимать много сил и времени. Поэтому в ряде случаев при проведении фундаментных и общестроительных работ целесообразно использовать уже готовую арматурную сетку.
Вычисление веса арматурной сетки
- Вычисление веса арматурной сетки может пригодиться вам для определения общего веса строительной конструкции, так и для расчета логистики – то есть способов доставки строительных материалов к месту возведения здания.

- Для того, чтобы произвести расчет веса арматурной сетки прежде всего необходимо узнать диаметр использованного металлического прута или проволоки, шаг между проволокой или прутками и конфигурацию ячеек.
- Так, шаг между проволокой или прутками может оставлять от 5 до 25 сантиметров. При создании арматурной сетки может использоваться как проволока диаметром от 3 миллиметров, так и арматурный металлический пруток диаметром до 12 миллиметров.
- При маркировке сетки используются стандартные обозначения, которые помогут вам вычислить вес арматурной сетки.
- Так, если арматурная сетка обозначена маркировкой «150х150х5», то это обозначает, что данное изделие имеет ячейку квадратной конфигурации 15 на 15 сантиметров и изготовлена из проволоки толщиной в 5 миллиметров.
- Для того, чтобы вычислить вес арматурной сетки можно воспользоваться таблицей, приведенной в нашей статье.
Обратите внимание, что разные производители могут использовать и нестандартные размеры арматурной сетки.
В этом случае необходимо рассчитывать ее вес индивидуально, с применением специальных формул. Хорошим решением будет использование для такого расчета математических электронных таблиц.
Кроме того, арматурная сетка может выпускаться и с различными покрытиями. Так, ряд предприятий выпускает оцинкованную арматурную сетку. Такая сетка имеет несравнимо более долгий срок службы и может использоваться и для наружных отделочных работ. Например, для создания заборов или ограждений.
| Диаметр (мм) | Вес кг/метр |
| 5,5 мм | 0,187 |
| 6 мм | 0,222 |
| 8 мм | 0,395 |
| 10 мм | 0,617 |
| 12 мм | 0,888 |
| 14 мм | 1,210 |
| 16 мм | 1,580 |
| 18 мм | 2,000 |
| 20 мм | 2,470 |
| 22 мм | 2,980 |
| 25 мм | 3,850 |
| 28 мм | 4,830 |
| 32 мм | 6,310 |
| 36 мм | 7,990 |
| 40 мм | 9,870 |
| 45 мм | 12,480 |
| 50 мм | 15,410 |
Очевидно, что при расчете веса в погонных метрах, вам также необходимо воспользоваться таблицей. К примеру, масса 1 метра 12 мм арматуры равняется 0,88 кг.
К примеру, масса 1 метра 12 мм арматуры равняется 0,88 кг.
Количество метров арматуры в одной тонне определяется при помощи следующей таблицы:
| Диаметр (мм) | Метров в одной тонне |
| 5,5 мм | 5347 |
| 6 мм | 4504 |
| 8 мм | 2531 |
| 10 мм | 1620 |
| 12 мм | 1126 |
| 14 мм | 826 |
| 16 мм | 633 |
| 18 мм | 500 |
| 20 мм | 405 |
| 22 мм | 335 |
| 25 мм | 260 |
| 28 мм | 207 |
| 32 мм | 158 |
Калькулятор для расчета веса арматурной сетки
Перевести арматуру из метров в килограммы. Онлайн калькулятор расчёта веса арматуры
Сферой применения арматуры является строительная индустрия. Данный вид металлоизделий производится в форме прутьев, используемых в качестве основной детали, служащей усилению железобетонных конструкций. Металл принимает на себя основную нагрузку на растяжение и изгиб, позволяя придавать сооружению из железобетона прочность, надёжность и долговечность.
Металл принимает на себя основную нагрузку на растяжение и изгиб, позволяя придавать сооружению из железобетона прочность, надёжность и долговечность.
Характеристики металлических стержней А12
Наибольшей востребованностью обладает арматура сечением 12 мм, благодаря удобству и лёгкости. А при вязке каркасов проявляется необходимая жесткость изделия. При строительстве загородных кирпичных домов применяется ленточный фундамент, технология возведения которого требует использования арматуры с малым диаметром. В подобных случаях наиболее пригодны двенадцатимиллиметровые стержни.
В процессе производства арматурных стержней с маркировкой «А12» выполняется ГОСТ 5781-82. Характеристики арматуры А12 по назначению подразделяются на напрягаемые и не подлежащие напряжению. В зависимости от специфики технологического процесса, изделия классифицируются на следующие виды:
Виды арматуры в зависимости от технологии изготовления
- холоднотянутый – арматурная проволока, предназначенная для изготовления армированной сетки;
- горячекатанный – стальные стержни с округлым сечением, применяемые для армирования конструкций.

Такая продукция изготавливается из разных видов стали, выбор которых зависит от требований и области применения будущего изделия. Арматура с диаметром 12 мм встречается с гладким профилем, что соответствует классу А1 и с рифлёной поверхностью, соответствующей маркировке А3. Металлопрокат поставляется производителями в прутах или бухтах.
Сфера применения арматурных стержней
Двенадцатимиллиметровая арматура широко используется в следующих областях:
Применение арматуры 12 мм в строительстве
- каркасно-монолитное строительство;
- монтаж опорных каркасов;
- армирование бетонных конструкций;
- устройство навесов и лестниц.
Также металлические прутья могут использоваться в качестве анкера при заливке фундамента столбчатого типа. Металлопрокат 12 мм применяют с целью преодоления деформации, формирования основы каркаса, связки отдельных элементов, в том числе и с поперечным расположением.
Вес погонного метра
На вес арматурных изделий влияют различные факторы, среди которых наиболее существенными являются следующие:
- диаметр металлического стержня;
- разновидность поверхности – гладкая либо с поперечным рифлением;
- класс металла.

Российские специалисты для расчёта веса металлических изделий применяют специально разработанные таблицы, основа которых – ГОСТ Р-52544. В соответствии с данным Госстандартом, вес погонного метра арматуры 12 составляет 0,888 кг.
Без применения специальных таблиц рассчитать вес арматуры не составит большого труда. Вес равен объёму тела, умноженному на средний удельный вес. Объём рассчитывается по формуле: площадь сечения, умноженная на длину. Согласно стандартам, за единицу измерения принимается метр.
Таким образом, площадь сечения = Пи * радиус в квадрате (радиус равен половине диаметра). S = 3.14х0,006 2 = 0,00011304. Соответственно вес = 0,00011304х7850 = 0,8874 , где 7850 – стандартный показатель среднего удельного веса двенадцатимиллиметровой арматуры.
Если под рукой имеется доступ к интернету, то рассчитать массу 1 метра 12 мм арматуры ещё проще, с помощью специальных калькуляторов, позволяющих произвести вычисления армирующих изделий любой марки и толщины.
Сколько метров двенадцатимиллиметровой арматуры в одной тонне
В таблицах, разработанных с учётом ГОСТа для арматуры, приведены следующие данные количества метров, содержащихся в тонне металлопроката:
- диаметр 5 миллиметров – 5347 метров;
- 6 мм – 4504 м;
- 8 – 2531;
- 10 – 1620;
- 12 – 1126;
- 14 – 826;
- 16 – 633.
Из выдержки табличных значений видно, что в одной тонне содержится 1126 метров арматуры с сечением 12 мм. Стандартизированные показатели направлены на облегчение процесса расчёта количества арматурных прутьев, необходимых для создания различных видов фундамента или иных конструкций.
Достоинства арматуры 12 мм
Двенадцатимиллиметровые металлические изделия обладают рядом достоинств, проявляющихся в следующих областях:
- высокий уровень прочности каркасов, выполненных с применением арматурных прутьев;
- достаточная пластичность материала;
- минимальный риск формирования коррозийных повреждений;
- высокая степень устойчивости к таким воздействиям, как химические, термические, механические;
- широкие возможности выполнения различных конфигураций каркасов;
- использование в напряженных железобетонных сооружениях.

Результаты расчётов, осуществляемых с помощью таблиц, формул и калькуляторов, являются усредненными значениями, так как в действительности арматурные прутья обладают не идеально круглым сечением. Для определения необходимого количества металлопроката полученных данных будет достаточно.
Важным моментом при расчётах является тот факт, что расчётный и фактический вес арматуры 12 мм могут отличаться друг от друга. Несмотря на тщательный контроль ГОСТ, металлические прутья изготавливаются из различных типов стали и с разными поверхностями, в связи с чем отклонение значений варьируется в диапазоне 0,2–3%.
Железобетон сегодня является самым распространенным материалом, используемым при строительстве многоэтажных зданий, дорог, тоннелей, мостов и любых других объектов. Арматура является важной составляющей таких конструкций – не армированный бетон, хотя и выдерживает значительные нагрузки на сжатие, практически не работает на изгиб и растяжение, разрушаясь при сравнительно небольших нагрузках. Но использование металлических прутов – обычных или предварительно напряженных – позволяет устранить этот недостаток. Нередко строители оказываются в ситуациях, когда им нужно узнать вес арматуры, для произведения расчетов необходимого количества материала для строительства. В этом им поможет таблица весов арматуры. Её вы найдете ниже в статье, в арматурной таблице, представлены значение массы металлических прутов всех диаметров.
Но использование металлических прутов – обычных или предварительно напряженных – позволяет устранить этот недостаток. Нередко строители оказываются в ситуациях, когда им нужно узнать вес арматуры, для произведения расчетов необходимого количества материала для строительства. В этом им поможет таблица весов арматуры. Её вы найдете ниже в статье, в арматурной таблице, представлены значение массы металлических прутов всех диаметров.
Разумеется, в первую очередь масса прута зависит от толщины. Чем больше диаметр, тем больше будет и вес. Сегодня при строительстве чаще всего применяются металлические пруты диаметром от 6 до 80 миллиметров. Масса 1 м арматуры, самой тонкой, весит всего 222 грамма, в то время как для самой толстой этот показатель составляет 39,46 килограмма. Как видите – разница огромна. Поэтому знание веса арматуры также не будет лишним при расчете давления конструкции на основание – несколько неучтенных тонн нагрузки может губительно сказаться на надежности и долговечности любой постройки.
Сколько весит арматура
Для того чтобы узнать арматурный вес, проще и удобнее всего воспользоваться специальной таблицей, представленной ниже.
Таблица веса арматуры
| Диаметр, мм | Вес 1 метра арматуры, кг | Погонных метров в тонне |
|---|---|---|
| 6 | 0,222 | 4504,5 |
| 8 | 0,395 | 2531,65 |
| 10 | 0,617 | 1620,75 |
| 12 | 0,888 | 1126,13 |
| 14 | 1,21 | 826,45 |
| 16 | 1,58 | 632,91 |
| 18 | 2 | 500 |
| 20 | 2,47 | 404,86 |
| 22 | 2,98 | 335,57 |
| 25 | 3,85 | 259,74 |
| 28 | 4,83 | 207,04 |
| 32 | 6,31 | 158,48 |
| 36 | 7,99 | 125,16 |
| 40 | 9,87 | 101,32 |
| 45 | 12,48 | 80,13 |
| 50 | 15,41 | 64,89 |
| 55 | 18,65 | 53,62 |
| 60 | 22,19 | 45,07 |
| 70 | 30,21 | 33,1 |
| 80 | 39,46 | 25,34 |
Все данные, указанные в этой таблице, в полной мере соответствуют действующему ГОСТу. Погрешность может составлять максимум несколько процентов – подобные ошибки не доставят значительных хлопот и точно не станут причиной повреждения конструкции.
Погрешность может составлять максимум несколько процентов – подобные ошибки не доставят значительных хлопот и точно не станут причиной повреждения конструкции.
Имея таблицу под рукой, можно быстро рассчитать вес арматуры, например, диаметром 32 мм. Найдите соответствующий диаметр в первом столбце и тут же узнаете, что её масса составляет 6,32 кг на 1м, а тонна включает в себя 158,48 метра.
Зачем нужно знать вес?
Часто у профессиональных строителей возникает вопрос – каков вес погонного метра арматуры. Зачем им это нужно? Дело в том, что при закупке прутов для возведения крупных сооружений, она покупается не поштучно, как при индивидуальном строительстве, а тоннами. Но сложно рассчитать, на сколько хватит определенной массы материала, если не знать, сколько весит метр арматуры. Знание же общей массы и удельного веса арматуры, 1 метра, можно за считанные секунды произвести простейшие расчеты, получив общую протяженность металлических стержней. Для этого, берём всю массу необходимых прутов, и делим на вес 1 погонного метра.
Пример расчета
Для армирования балок необходимо 2,5 тонны прутов 25 диаметра. Берем из таблицы величину массы 1 метра, равно 3,85 кг. Далее переводим тонны в килограммы, умножаем на 1000, будет 2500 кг, и делим на 3,85, получаем 649 метров материала. Стандартная длинна металлического прута 11,7 м, чтобы узнать необходимое количество стержней, делим 649 на 11,7, получаем 55,5 шт. Таким образом можно посчитать количество стержней с любым сечением. Это поможет, особенно в частном строительстве, для проверки, правильное ли количество материала вам доставили.
Также может иметь место обратная ситуация. Специалист знает, какое количество материала ему нужно, а также знает оптимальный диаметр. Узнав теоретический вес метра арматуры, ему достаточно умножить это число на общую длину необходимых металлических прутов, чтобы определить, какое количество материала нужно для строительства.
В основном арматурные стержни используют для укрепление бетона. С них вяжут сетку, так она принимает силу растяжения, которая идет на бетон. В строительном секторе, очень часто используют прокат именно с размером сечения 10 миллиметров. И, что бы создать армокаркас или же сетку, нужно знать точный вес арматуры 10 мм. за метр. В этой статье ми поговорим именно об этом стальном продукте.
В строительном секторе, очень часто используют прокат именно с размером сечения 10 миллиметров. И, что бы создать армокаркас или же сетку, нужно знать точный вес арматуры 10 мм. за метр. В этой статье ми поговорим именно об этом стальном продукте.
Вес арматуры всегда обусловлен стандартом ГОСТ5781-82, он говорит какая должна бить масса и другие параметры. Арматура выпускается в двух видах:
- горячекатанным;
- холодночекатанным.
Сам же прокат создается в виде металлических стержней или прутьев.
Арматура 10 мм вес 1 метраДля оценки стоимости строительства, или же готовых объектов, нужно знать точную массу армированных конструкций. Узнать сколько весит арматура 10 мм. можно простым способом: суммируем длину и умножаем на погонный вес нашего металлопроката.
Для того что бы узнать массу погонного м, нужно свериться с таблицей, в которой выведены все размеры их вес и количество метров в тонне.
Таблица веса и количества метров в тонне арматуры диаметром 10 мм.
Вес 1 метра арматуры размером десять миллиметров представлен в таблице соотношения диаметра и массы одного м. Зная вес арматурной стали согласно ГОСТ 5781-82 можно оценить коэффициент проката (отношение массы арматуры к объему бетона) и вычислить, сколько на понадобиться металлических прутьев (на куб бетона).
Сколько весит арматура 10 мм? Таблица.
Имея под рукой выше изложенную таблицу, Вы всегда будете знать точное количество и массу этого стального продукта с нужным диаметром сечения. Что, не составит большого труда рассчитать стоимость, перед покупкой, тем самим уберечь себя от лишних затрат.
Как произвести самостоятельный расчет?Без табличных данных общий вес арматурной сетки или вес одного погонного м. можно рассчитать на онлайн калькуляторе, или сделать это самостоятельно. Для этого длину армирующих прутьев сетки, например, площадью 1м2, умножают на удельную массу одного погонного метра армостержней. Объем стали для 1 м. исследуемого металлического цилиндра равняется 1 метр x (∏ x D2 x / 4).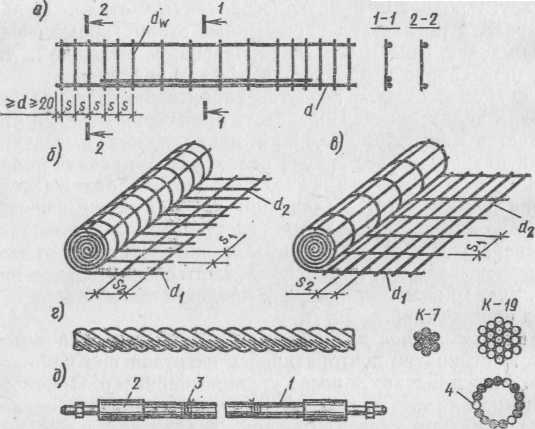
Вес арматурного стержня будет равен производному от полученного объема и удельной массы арматуры, которая равняется 7850 кг/м3. Эта упрощенная методика позволяет рассчитать массу в килограммах одного метра арматурных стержней, а также перевести вес в единицы длины (метры).
Изготовление арматурной стали регламентируется стандартом ГОСТ 5781-82. В документе прописаны технические требования и условия, классификация, сортамент, методы испытаний и другие требования к изделию. Ниже представлены некоторые справочные таблицы из ГОСТ 5781-82, с помощью которых можно узнать теоретическую массу одного метра арматуры. Вес изделия также можно рассчитать самостоятельно, или с помощью этого калькулятора.
Таблица: Теоретическая масса 1 погонного метра арматуры по ГОСТ 5781-82
Номер, | Диаметр d, мм | Площадь поперечного сечения, см | Вес 1 метра, кг | Количество метров в тонне |
Арматура 6 | ||||
Арматура 8 | ||||
Арматура 10 | ||||
Арматура 12 | ||||
Арматура 14 | ||||
Арматура 16 | ||||
Арматура 18 | ||||
Арматура 20 | ||||
Арматура 22 | ||||
Арматура 25 | ||||
Арматура 28 | ||||
Арматура 32 | ||||
Арматура 36 | ||||
Арматура 40 | ||||
Арматура 45 | ||||
Арматура 50 | ||||
Арматура 55 | ||||
Арматура 60 | ||||
Арматура 70 | ||||
Арматура 80 |
Для чего нужен онлайн калькулятор?
Мы предлагаем сервис, который содержит два в одном: калькулятор веса арматуры по массе и по метру.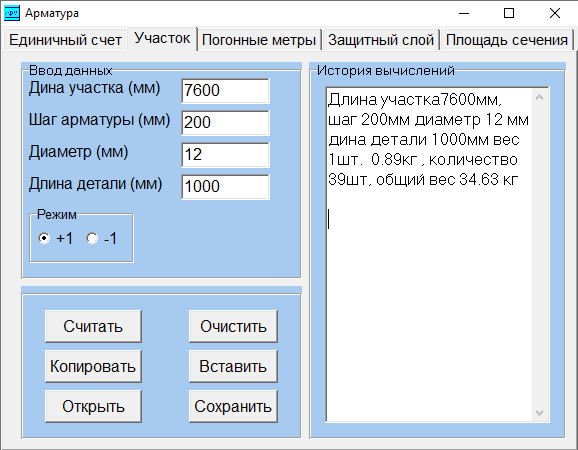 Таким образом, можно узнать длину готового изделия, зная вес, или наоборот – узнать вес изделия определённой длины. Онлайн калькулятор арматуры пригодится при составлении проектно-сметной документации и расчётов металлических конструкций. С его помощью также можно узнать стоимость готового изделия, указав цену за метр или тонну.
Таким образом, можно узнать длину готового изделия, зная вес, или наоборот – узнать вес изделия определённой длины. Онлайн калькулятор арматуры пригодится при составлении проектно-сметной документации и расчётов металлических конструкций. С его помощью также можно узнать стоимость готового изделия, указав цену за метр или тонну.
Как пользоваться калькулятором?
- Выберите метод вычисления (по длине или по массе).
- Выберите диаметр арматуры из всплывающего списка.
- Введите значение «Масса» или «Количество метров».
- При необходимости, укажите цену одного метра или тонны.
- Нажмите красную кнопку «Рассчитать».
- В левом верхнем углу, в колонке «Результаты расчёта» вы увидите полученные данные.
Как рассчитать вес самостоятельно?
Зная номинальный диаметр и плотность материала, можно самостоятельно выполнить расчет веса арматуры. Считается он по формуле m = D х D х Pi / 4 х ro , согласно которой масса одного метра арматуры равняется теоретической массе круга с тем же диаметром. Значения из формулы:
Значения из формулы:
- m – искомая масса арматуры.
- D — номинальный диаметр арматуры.
- ro — плотность материала.
- Pi – число Пи.
Плотность регламентированной ГОСТ-ом арматуры из углеродистой стали составляет 7850.00 кг/м 3 .
Как узнать фактический вес арматуры?
Как и справочные таблицы, калькулятор арматуры рассчитывает теоретический вес изделия. ГОСТ допускает отклонения геометрических размеров изделия от номинальных. Узнать фактический вес можно путём взвешивания арматуры определённой длины. Точная информация о массе и других характеристиках арматуры указана в паспорте изделия от производителя.
Ответ на вопрос, сколько метров арматуры в 1 тонне, интересует как проектировщиков, так и строителей. Данная информация нужна для определения массы и стоимости сооружения, а также для правильной организации работ при закупке и доставке на строительную площадку. Эта задача возникает из-за того, что результаты прочностных расчётов прутков представлены в метрах, а чтобы купить их, необходимы данные в тоннах.
Разновидности
Для фундаментов, железобетонных конструкций, газоблочных домов применяют сталь круглого и периодического профиля. Последняя имеет вид цилиндрических стержней с поперечными выступами, образованными по винтовой линии и двумя продольными рёбрами. Имеется вариант, в которых выполнены правый и левый заходы на противоположных сторонах прутьев для улучшения сцепления с бетоном (используется для сталей высокой прочности).
Основной величиной, по которой определяется количество арматуры, это её номинальный диаметр (d), независимо от того, какая поверхность: гладкая или с различного вида рифлением. В соответствии со стандартами площади поперечного сечения периодического профиля (некруглые) и имеющие форму круга того же диаметра, идентичны. Следовательно, равны и их массы, приходящиеся на 1 метр.
Согласно ГОСТ 5781-82 выпускается горячекатаная – А1000 (буква А обозначает метод производства, а число – предел текучести в МПа):
По стандарту 10884-94 изготавливают термомеханически упрочнённые стержни:
Технология расчета
Известно несколько способов определения количества погонных метров прутьев в тонне (L):
- Используя формулу вычисления массы тела по известному объёму и плотности (ρ): L = (4∙1000)/(ρ∙π∙d 2) (1), где: ρ = 7850 кг/м 3 – плотность стального проката для теоретических расчётов, d – берётся в метрах, 1 тонна = 1000 кг.

- Используя данные по из соответствующих стандартов на изготовление.
Число погонных метров в одной тонне узнать достаточно просто: L = 1000/q, где q – масса 1 метра (кг/м).
Ниже приведено количество метров арматуры в тонне по этой методике и выражению (1).
| D, мм | L, м | ||
| ГОСТ 5781-82; 10884-94 | Р 52544-2006 | По (1) | |
| 4 | — | 10101,010 | 10137,250 |
| 5 | — | 6493,507 | 6487,840 |
| 6 | 4504,505 | 4504,505 | 4505,444 |
| 8 | 2531,646 | 2531,646 | 2534,312 |
| 10 | 1620,746 | 1623,377 | 1621,960 |
| 12 | 1126,126 | 1126,126 | 1126,361 |
| 14 | 826,446 | 827,815 | 827,530 |
| 16 | 632,911 | 633,714 | 633,578 |
| 18 | 500,000 | 500,500 | 500,604 |
| 20 | 404,858 | 405,515 | 405,490 |
| 22 | 335,571 | 335,120 | 335,115 |
| 25 | 259,740 | 259,538 | 259,513 |
| 28 | 207,039 | 206,868 | 206,882 |
| 32 | 158,479 | 158,403 | 158,394 |
| 36 | 125,156 | 125,156 | 125,151 |
| 40 | 101,317 | 101,368 | 101,372 |
| 45 | 80,128 | — | 80,096 |
| 50 | 64,893 | — | 64,878 |
| 55 | 53,619 | — | 53,618 |
| 60 | 45,065 | — | 45,054 |
| 70 | 33,102 | — | 33,101 |
| 80 | 25,342 | — | 25,343 |
По стандарту Р52544-2006 возможно производство номеров профилей арматурных прутьев, удельный вес которых не указан в нормативном документе (4,5; 5,5; 6,5; 7; 7,5; 8,5; 9; 9,5; 45; 50 мм). Как видно из сравнения расчётов по формуле (1) и данных, полученных на основании удельного веса, результаты несколько различаются (расхождения составляют 0,36-1,0 %). Чтобы купить необходимое количество стержней, применительно к размерам, не вошедшим в стандарт, оценка по формуле (1) вполне приемлема, особенно с учётом допусков на изготовление тонны проката.
Как видно из сравнения расчётов по формуле (1) и данных, полученных на основании удельного веса, результаты несколько различаются (расхождения составляют 0,36-1,0 %). Чтобы купить необходимое количество стержней, применительно к размерам, не вошедшим в стандарт, оценка по формуле (1) вполне приемлема, особенно с учётом допусков на изготовление тонны проката.
Помимо теоретических имеет место эмпирический метод определения числа метров армирующих изделий в тонне путём их непосредственного взвешивания. Данный способ является наиболее достоверным, а точность его зависит от погрешности используемых весов, например, подвесных крановых.
Главная » Водоснабжение » Перевести арматуру из метров в килограммы. Онлайн калькулятор расчёта веса арматуры
Калькулятор аксессуаров
Расчет арматуры
Калькулятор аксессуаров 1
Рассчитать общий вес арматуры, общую сумму, вес одного метра и одного стержня арматуры.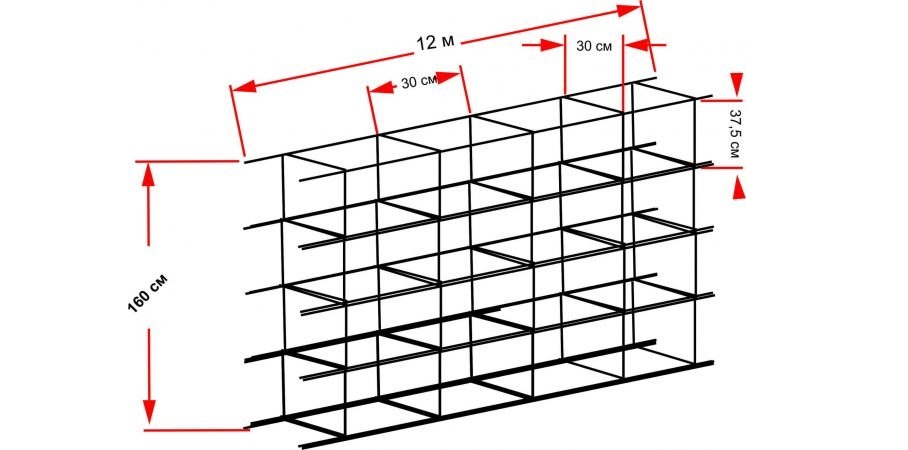
На известные диаметр и длину.
Калькулятор принадлежностей 2
Расчет общей длины арматуры, ее объема и количества стержней, стержней, веса одного метра и одного стержня.
По известному диаметру и общему весу.
Расчет основан на весе одного кубометра стали 7850 кг.
Расчет арматуры для домостроения
При строительстве Дома очень важно правильно рассчитать количество створок для фундамента. В этом вам поможет наша программа. С помощью калькулятора запорной арматуры можно, зная вес и длину штока, узнать общий вес задвижек или желаемое количество штоков и их общую длину. Эти данные помогут быстро и легко рассчитать количество арматуры для необходимых работ.Расчет арматуры для различных типов фундаментов
Для расчета арматуры необходимо знать и тип фундамента дома. Есть два распространенных варианта. Это ростверк и ленточный фундамент.Арматура для плитного фундамента
Плотный фундамент используется там, где на пучинистый грунт требуется установить тяжелый бетонный или кирпичный дом с большой массой бетонных перекрытий.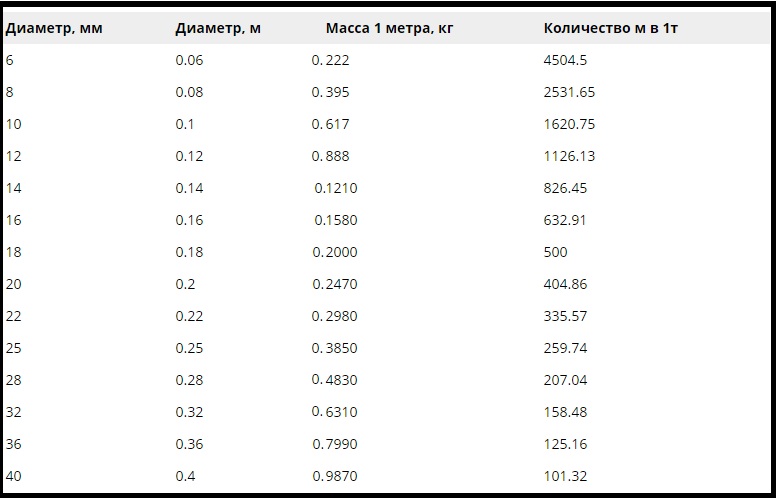 В таком случае фундамент требует усиления. Производится в двух зонах, каждая из которых состоит из двух слоев стержней, расположенных перпендикулярно друг другу.
В таком случае фундамент требует усиления. Производится в двух зонах, каждая из которых состоит из двух слоев стержней, расположенных перпендикулярно друг другу.Рассмотрим альтернативный расчет арматуры для плиты длиной 5 метров. Арматурные прутья располагают на расстоянии около 20 см друг от друга. Следовательно, на одну сторону потребуется 25 стержней. По краям пластины шпильки отсутствуют, это 23.
Теперь, зная количество стержней, можно рассчитать их длину. Здесь следует учесть, что стержни клапанов не должны доходить до краев 20 см, а, следовательно, исходя из длины пластин, длина каждого стержня составит 460 см.Поперечный слой при условии, что печь имеет квадратную форму, будет одинаковым. Мы также должны рассчитать количество фитингов, необходимых для соединения обеих зон.
Предположим, что расстояние между зонами 23 см. В этом случае одна перемычка между ними будет иметь длину 25 см, потому что еще два дюйма нужно для крепления крепления. Таких мостов в нашем случае будет 23 подряд, так как они есть в каждой ячейке на пересечении зон.
 Имея эти данные, мы можем перейти к расчету с помощью программы.
Имея эти данные, мы можем перейти к расчету с помощью программы.Арматура для ленточного фундамента
Ленточный фундамент применяют там, где в не слишком устойчивом грунте предполагается возведение жесткого дома. Представляет собой фундамент из бетонной или железобетонной ленты, протянутой по периметру здания и под основными несущими стенами. Армирование фундамента также производится в 2 зоны, но благодаря особенностям ленточного фундамента арматура на него расходуется значительно меньше, поэтому и стоимость будет дешевле.Правила подхвата арматуры примерно такие же, как и для плитного фундамента.Только стержни должны быть уже в 30-40 см от угла. И каждая перемычка должна на 2-4 см свисать с веточки, на которую она опирается. Расчет вертикальных перемычек по тому же принципу, что и при расчете необходимой длины арматуры для плитных фундаментов.
Учтите, что клапаны первого и второго корпусов должны иметь запас не менее 2-5 процентов.
Электрические машины — Якорь машины постоянного тока
Двигатель больше не работает со скоростью 1000 об/мин. Напряжение якоря указано по
Напряжение якоря указано по
\[E_A=k\фи \omega_m\]
я.е. напряжение является функцией \(k\phi\) и скорости. Поток является только функцией тока возбуждения, и поскольку в вопросе указаны напряжение и сопротивление возбуждения, первым шагом является определение тока возбуждения:
\[ V_F=I_F R_F \]
дает \(I_F=0,4A\)
Из таблицы в вопросе, когда: \(n_m=1000\text{rpm}\) и \(I_F=0.4A\) тогда \(E_A=102V\). Нам нужно найти \(E_A\) для случая, когда \(n_m=1200\text{rpm}\) и \(I_F=0.4А\)
Есть два возможных подхода:
- В обоих случаях ток возбуждения постоянен, поэтому поток будет постоянным. Напряжение якоря будет пропорционально скорости:
\[ E_A |_{1200}=E_A |_{1000}\фракция{1200}{1000} \]
Подача \(E_A=122,4 В\) - Используя уравнение напряжения якоря и данные таблицы, найдите \(k\phi\) при \(I_F=0,4A\). Данные в таблице дают \(E_A|_{1000} = 102 В\) при \(n_m=1000 об/мин\) и, следовательно, \(\omega_m=1000\frac{2\pi}{60} = \frac{100 \пи}{3}\).
 Следовательно
Следовательно\[ \begin{выровнено} k\phi |_{I_F =0,4} &=\frac{102}{\frac{100 \pi}{3}} =\frac{306}{100}\frac{1}{\pi}\\ k\phi |_{I_F =0,4} &=0,974 \end{выровнено} \]
Теперь при 1200 об/мин напряжение якоря можно найти непосредственно из уравнения напряжения якоря:\[ \begin{выровнено} E_A |_{1200} &=k\phi |_{I_F =0,4} \omega_m \\ \omega_m & = 1200\frac{2 \pi}{60} = 40\pi \end{выровнено} \]
Давая \(E_A=122.2 — 60 И_А + 4160 = 0 \]Решение квадратичного уравнения для тока якоря дает два значения: \(I_A=616A\) или \(IA=33,75A\). Правильным ответом будет тот, который приводит к наименьшим потерям мощности,\(I_A=33,75A\).
В этот момент можно найти потери в якоре, но это машина с независимым возбуждением, и важно не забудьте учесть поток мощности в цепи возбуждения. Поэтому необходимо найти ток цепи возбуждения \(I_F\), и опять же, есть несколько подходов к этому решению
- Найдите напряжение якоря при 1450 об/мин \(E_A|_{1450}\), уменьшите до \(E_A |_{1000}\) и используйте таблицу для поиска \(I_F\)
- Рассчитайте крутящий момент, чтобы получить \(k=phi\), а затем рассчитайте соответствующее значение в таблице
\[ V_T = E_A+ I_A R_A \]
дает\(E_A|_{1450}=123. 25А\)
25А\)\[ E_A\big|_{1000}=E_A\big|_{1450}\frac{1000}{1450} \]
дает \(E_A\ |_{1000}=85.0V\), что, согласно таблице, соответствует току возбуждения \(I_F=0.3A\)\[ \begin{выровнено} P_{conv} & =\tau\omega_m\\ \tau& = \frac{4160}{\frac{1450\pi}{30}} = 27,4 Нм \\ k \ phi & = \ frac {\ tau} {I_A} = 0,812 \\ E_A|_{1000} &=k\phi \frac{1000 \pi}{30} \end{выровнено} \]
что дает \(E_A\ |_{1000}=85.2 R_F= 235Вт\\ P_{FW}&=0\\ \eta &=\frac{4160}{4395} \\ \end{выровнено} \]дает \(\eta=94.7\%\)
Emetor — Калькулятор обмотки электродвигателя
Внимание! Emetor лучше всего работает с включенным JavaScript. Включите JavaScript в настройках браузера и повторите попытку.Калькулятор обмотки позволяет быстро и удобно найти оптимальную схему обмотки для вашего электродвигателя.Вы можете исследовать трехфазные обмотки с целыми пазами, дробными пазами и сосредоточенными обмотками, как с одинарными, так и с двойными слоями обмотки, где это необходимо.
 Вы можете сравнить максимальный основной коэффициент обмотки для различных комбинаций количества полюсов и количества пазов, отобразить схему обмотки для различных пролетов катушек или оценить спектр гармоник коэффициента обмотки.
Вы можете сравнить максимальный основной коэффициент обмотки для различных комбинаций количества полюсов и количества пазов, отобразить схему обмотки для различных пролетов катушек или оценить спектр гармоник коэффициента обмотки.Emetor отказывается от каких-либо гарантий, включая, помимо прочего, подразумеваемые гарантии товарного состояния, точности или пригодности для какой-либо конкретной цели.Ни при каких обстоятельствах компания Emetor не несет ответственности перед какой-либо стороной за любой ущерб, возникший в результате использования информации из этого калькулятора намотки.
Определить количество слотов и количество полюсов
Для начала выберите примерный диапазон количества полюсов и количество слотов, которые вас интересуют. После обновления таблицы выпадающий список ниже позволяет выбрать, отображать ли количество слотов на полюс на фазу, максимально возможный основной коэффициент обмотки, количество симметрий обмотки или наименьшее общее кратное между количеством полюсов и количеством пазов в таблице.

2 4 6 8 10 12 14 9 01059 8 6 9 12 15 18 21 Исследование и редактирование конкретных схем обмотки
Нажмите на ячейку в приведенной выше таблице, чтобы выяснить, какие схемы обмотки возможны для данного количества полюсов и количества пазов.
Нажмите на строку таблицы ниже, чтобы отобразить и отредактировать схему обмотки. Теперь также можно загрузить выбранные детали обмотки.

# Поляки Слоты Слои Пролет катушки Участок для столбов Периодичность Коэффициент намотки Отображение и сравнение гармоник обмотки
Доступны три различных типа диаграмм, которые можно выбрать ниже.
Вы можете скрыть гармоники обмотки определенной схемы обмотки, щелкнув соответствующую метку, расположенную справа от диаграммы. Используйте колесо мыши, чтобы увеличить график.
Формулы и уравнения генератора постоянного тока
Формулы генераторов постоянного тока и шунтовых генераторов, КПД, уравнения мощности и ЭДС
Следующие основные формулы и уравнения генератора постоянного тока можно использовать для проектирования, упрощения и анализа основных схем генератора для определения мощности, эффективности, напряжения и тока, генерируемой ЭДС, крутящего момента, потерь и т. д.
д.
Шунтовой генератор: Напряжение на клеммах:V = E а – I а R а
Где
Терминальный ток:I a = I f + I L
, где I f — ток возбуждения, а I L — ток нагрузки
Полевой ток:I f = V / R ш
Где
- I f — ток возбуждения
- Р Ш Шунт Полевой Сопротивление
ЭДС, генерируемая на проводник в генераторе постоянного тока:
Где- Z = количество проводников
- P = количество полюсов
- N = скорость ротора в об/мин
- A = количество параллельных путей
ЭДС, генерируемая на пути для волновой обмотки и обмотки внахлестку;
Таким образом, обобщенное уравнение для генерируемой ЭДС генератора постоянного тока:E г = kΦω
Где
- K = ZP/2πA = константа машины постоянного тока
- ω = 2πN/60 = угловая скорость в рад в секунду
Похожие сообщения:
Крутящий момент генератора постоянного тока:крутящий момент генератора прямо пропорционален току якоря и определяется как:
T = k f ΦI a
Где
- K f — константа, основанная на конструкции машин .
- Φ — магнитный поток
- ω — угловая скорость

Генерируемая мощность и мощность нагрузки
Где N — скорость вращения в минуту (об/мин)Мощность, вырабатываемая шунтирующим генератором, определяется как:
P г = ωT = E a I a
P L = VI L
Где I L — ток нагрузки
Генератор серии
: Напряжение на клеммах:V = E a – (I a R a + I a R se )
V = E a – I a (R a + R se )
Где
- E a — напряжение, индуцированное якорем
- I a — ток якоря
- R a — сопротивление якоря
- R se — это серия полевого сопротивления .

Последовательный ток возбуждения равен току якоря;
I a = I se
Напряжение и крутящий момент, индуцируемые якорем:Индуцированное напряжение якоря E a пропорционально скорости и току якоря, тогда как крутящий момент T последовательного генератора прямо пропорционален квадрату тока якоря и определяется по формуле:
E а = k f ΦωI а
T = k f Φ I a 2
Где
- K f — константа, основанная на конструкции машин .
- Φ — магнитный поток
- ω — угловая скорость
Генерируемая мощность и мощность нагрузки
Где N — скорость вращения в минуту (об/мин)Мощность, вырабатываемая последовательным генератором, определяется как:
P г = ωT = E a I a
P L = VI L
Где I L — ток нагрузки
Входная мощность :P в = ωT
Где
- ω — угловая скорость якоря
- T — приложенный крутящий момент
P con = P in – Блуждающие потери – механические потери – потери в сердечнике
P con = E a I a
Где
- E a наведенное напряжение
- I a ток якоря
P вых = P кон – Электрические потери (I 2 R)
P вне = VI L
Где
- В — напряжение на клеммах
- I L ток нагрузки
Эффективность генератора постоянного тока:
Механический КПД:Похожие сообщения:
Электрическая эффективность: Общая эффективность:
Где- P out полезная выходная мощность
- P a — потери в меди в якоре
- P f — потери в меди в поле
- P k постоянные потери, содержащие потери в сердечнике и механические потери
Эффективность генератора постоянного тока максимальна, когда;
Переменная потеря мощности = Постоянная потеря мощности
Потери в меди = потери в сердечнике и механические потери
Потери в меди (I 2 R), такие как потери в якоре и обмотке возбуждения, являются переменными потерями, поскольку они зависят от тока.
 В то время как потери в сердечнике, такие как гистерезис и потери на вихревые токи, механические потери, такие как потери на трение, являются постоянными потерями.
В то время как потери в сердечнике, такие как гистерезис и потери на вихревые токи, механические потери, такие как потери на трение, являются постоянными потерями.Связанные формулы и уравнения Сообщений:
Учебное пособие по двигателю постоянного тока. Расчеты двигателей постоянного тока без сердечника с щеточными двигателями
Расчеты двигателей постоянного тока без сердечника
При выборе щеточного электродвигателя постоянного тока без сердечника для применения или при разработке прототипа с питанием необходимо учитывать несколько основных физических принципов электродвигателя, которые необходимо учитывать для создания безопасной, хорошо функционирующей и достаточно мощной прецизионной приводной системы.В этом документе мы предоставили некоторые важные методы, формулы и детали расчетов для определения выходной мощности двигателя без сердечника, кривую скорость-момент двигателя, графики тока и КПД, а также теоретические холодные расчеты, которые оценивают производительность двигателя.
Двигатели постоянного тока
являются преобразователями, поскольку они преобразуют электрическую энергию ( P в ) в механическую энергию ( P из ). Частное обоих членов равно КПД двигателя.Потери на трение и потери в меди приводят к общим потерям мощности ( P потери ) в джоулях/сек (потери в железе в двигателях постоянного тока без сердечника незначительны). Есть дополнительные потери из-за повышения температуры, но о них мы поговорим ниже:
В физике мощность определяется как скорость выполнения работы. Стандартной метрической единицей мощности является «Ватт» Вт. Как рассчитывается мощность? Для линейного движения мощность есть произведение силы на расстояние в единицу времени P = F · (d/t) .Поскольку скорость — это расстояние во времени, уравнение принимает вид P = F · s . В случае вращательного движения аналогичный расчет мощности представляет собой произведение крутящего момента и углового расстояния в единицу времени или просто произведение крутящего момента и угловой скорости.

где:
P = мощность в W
м = крутящий момент в NM
F = сила в N
D = Расстояние в M
T = Время в S
Ω RAD = Угловая скорость в рад/сОбозначение крутящего момента обычно представляет собой строчную греческую букву «τ» (тау) или иногда просто букву «T» .Однако когда его называют моментом силы, его обычно обозначают буквой «М» .
Европейская номенклатура часто использует строчную букву « n » для обозначения скорости относительно оси. Обычно « n » выражается в оборотах в минуту или об/мин.
При расчете механической мощности важно учитывать единицы измерения. При расчете мощности, если « n » (скорость) находится в мин -1 , то вы должны преобразовать его в угловую скорость в единицах рад/с .
 Это достигается путем умножения скорости на коэффициент преобразования единиц 2π/60 . Кроме того, если « M » (крутящий момент) выражается в мНм , то мы должны умножить его на 10 -3 (разделить на 1 000), чтобы преобразовать единицы измерения в Нм для целей расчета.
Это достигается путем умножения скорости на коэффициент преобразования единиц 2π/60 . Кроме того, если « M » (крутящий момент) выражается в мНм , то мы должны умножить его на 10 -3 (разделить на 1 000), чтобы преобразовать единицы измерения в Нм для целей расчета.Где:
n = скорость в мин -1
M = крутящий момент в мНмПредположим, что необходимо определить мощность, которую должен обеспечить конкретный двигатель 2668W024CR при работе в холодном состоянии с крутящим моментом 68 мНм при частоте вращения 7 370 мин -1 .Произведение крутящего момента, скорости и соответствующего коэффициента преобразования показано ниже.
Расчет начальной потребляемой мощности часто используется в качестве предварительного шага при выборе двигателя или мотор-редуктора. Если известна механическая выходная мощность, необходимая для данного приложения, то можно изучить максимальную или непрерывную номинальную мощность для различных двигателей, чтобы определить, какие двигатели являются возможными кандидатами для использования в приложении.

Ниже представлен метод определения параметров двигателя на примере двигателя постоянного тока без сердечника 2668W024CR.Сначала мы объясним более эмпирический подход, затем проведем теоретический расчет.
Одним из широко используемых методов графического построения характеристик двигателя является использование кривых скорости вращения. Хотя использование кривых крутящий момент-скорость гораздо чаще встречается в технической литературе для более крупных машин постоянного тока, чем для небольших устройств без сердечника, этот метод применим в любом случае.
Обычно кривые крутящий момент-скорость создаются путем построения графиков скорости двигателя, тока двигателя, механической выходной мощности и КПД в зависимости от крутящего момента двигателя.В следующем обсуждении будет описано построение набора кривых крутящий момент-скорость для типичного двигателя постоянного тока на основе серии измерений необработанных данных.
2668W024CR имеет номинальное напряжение 24 В.
 Если у вас есть несколько основных единиц лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.
Если у вас есть несколько основных единиц лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.Шаг 1: Измерьте основные параметры
Многие параметры можно получить непосредственно с помощью контроллера движения, например, одного из контроллеров движения FAULHABER MC3.Большинство производителей контроллеров предлагают программное обеспечение, такое как FAULHABER Motion Manager, которое включает в себя функцию записи кривой, отображающую напряжение, ток, положение, скорость и т. д. Они также могут предоставить точный моментальный снимок работы двигателя в мельчайших деталях. Например, контроллеры движения семейства MC3 (MC 5004, MC 5005 и MC 5010) могут измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.
Если контроллер с возможностью записи трассировки недоступен, мы также можем использовать базовое лабораторное оборудование для определения характеристик двигателя в условиях останова, номинальной нагрузки и без нагрузки.
 Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем.Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.
Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем.Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.Теперь увеличьте крутящий момент двигателя до точки где происходит застой. В остановленном состоянии измерьте крутящий момент от тормоз и ток двигателя. Ради этого обсуждения предположим, что муфта не добавляет нагрузки к двигатель и что нагрузка от тормоза не содержат неизвестные фрикционные компоненты. Это также полезно в этот момент для измерения конечного сопротивления мотор.Измерьте сопротивление, связавшись с двигателем клеммы омметром.
 Затем вращайте вал двигателя
и сделайте еще одно измерение. Измерения
должны быть очень близки по значению. Продолжайте вращать вал
и сделайте не менее трех измерений. Это обеспечит
что измерения проводились не в точке
минимальный контакт на коммутаторе.
Затем вращайте вал двигателя
и сделайте еще одно измерение. Измерения
должны быть очень близки по значению. Продолжайте вращать вал
и сделайте не менее трех измерений. Это обеспечит
что измерения проводились не в точке
минимальный контакт на коммутаторе.Теперь мы измерили:
N 0 = беззащитный скорость
I 0 = NO-нагрудный ток
м ч = стойло крутящий момент
R = сопротивление клеммаШаг 2: Постройте график зависимости тока отКрутящий момент и скорость против крутящего момента
Вы можете построить график с крутящим моментом двигателя по оси абсцисс (горизонтальная ось), скоростью по левой оси ординаты (вертикальная ось) и током по правой стороне ординаты. Масштабируйте оси на основе измерений, сделанных на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) к току останова на правой стороне ординаты (момент останова и ток останова).
 Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя.Наклон этой линии представляет собой константу тока k I , которая представляет собой константу пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мНм). Обратной величиной этого наклона является постоянная крутящего момента k M (в единицах крутящего момента на единицу тока или мНм/А).
Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя.Наклон этой линии представляет собой константу тока k I , которая представляет собой константу пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мНм). Обратной величиной этого наклона является постоянная крутящего момента k M (в единицах крутящего момента на единицу тока или мНм/А).Где:
k I = постоянная тока
k M = постоянная моментаДля целей данного обсуждения предполагается, что двигатель не имеет внутреннего трения.На практике момент трения двигателя M R определяется путем умножения постоянной момента k M двигателя на измеренный ток холостого хода I 0 .
 Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.Где:
M R = Момент тренияШаг 3: График Power vs.Крутящий момент и эффективность по сравнению с крутящим моментом
В большинстве случаев можно добавить две дополнительные вертикальные оси для отображения зависимости мощности и эффективности от крутящего момента. Вторая вертикальная ось обычно используется для эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения эффективность в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).
Составьте таблицу механической мощности двигателя в различных точках от холостого хода до крутящего момента при остановке.
 Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.
Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.Пример таблицы расчетов для двигателя 2668W024CR показан в Таблице 1. Затем каждая расчетная точка для мощности наносится на график. Результирующая функция представляет собой параболическую кривую, как показано ниже на графике 1. Максимальная механическая мощность возникает примерно при половине крутящего момента срыва.Скорость в этот момент составляет примерно половину скорости холостого хода.
Составьте таблицу КПД двигателя в различных точках от скорости холостого хода до крутящего момента. Задано напряжение, прикладываемое к двигателю, и нанесен ток при различных уровнях крутящего момента. Произведение тока двигателя и приложенного напряжения представляет собой мощность, подводимую к двигателю.
 В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность.Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.
В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность.Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.Определения сюжета
- Синий = скорость в зависимости от крутящего момента ( n против M )
- Красный = ток против крутящего момента ( I против M ) против 9 η 0 зеленый = КПД M )
- Коричневый = мощность и крутящий момент ( P и . М )
Характеристики двигателя
Примечание. Обратите внимание, как изменяются все четыре сплошных графика в результате увеличения сопротивления в медных обмотках и ослабления выходной крутящий момент из-за повышения температуры. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.
Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.Ток нагрузки 2,79 А Напряжение нагрузки 24,11 В Температура обмотки двигателя 140,23 °С Температура корпуса двигателя 105,03 °С Скорость двигателя 7370 мин -1 Требуемый момент нагрузки 68 мНм Выходная мощность 52,48 Вт Эффективность (в целом) 77,97 % Примечание.
 Из-за нехватки места отображается пример расчета для одной точки.
Из-за нехватки места отображается пример расчета для одной точки.Теоретический расчет параметров двигателя
Другим полезным параметром при выборе двигателя является постоянная двигателя. Правильное использование этого показателя качества существенно сократит итерационный процесс выбора двигателя постоянного тока. Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую энергию в механическую.
Максимальный КПД достигается примерно при 10% крутящего момента двигателя. Знаменатель известен как резистивная потеря мощности.С некоторыми алгебраическими манипуляциями уравнение можно упростить до:
Пожалуйста, имейте в виду, что k m (постоянная двигателя) не следует путать с k M (постоянная момента). Обратите внимание, что нижний индекс константы двигателя записывается строчными буквами « м », а нижний индекс константы крутящего момента — заглавными буквами « M ».

Для щеточного или бесщеточного двигателя постоянного тока относительно небольшого размера соотношения, управляющие поведением двигателя в различных обстоятельствах, могут быть получены из законов физики и характеристик самих двигателей.Правило напряжения Кирхгофа гласит: «Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов». Применительно к двигателю постоянного тока, соединенному последовательно с источником питания постоянного тока, правило напряжения Кирхгофа может быть выражено как «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падения напряжения на сопротивлении обмоток и противо-ЭДС, создаваемой двигателем».
Где:
U = Напряжение питания в В
I = Ток в А
R = Сопротивление клемм в Ом
U E = Back-09Противо-ЭДС, создаваемая двигателем, прямо пропорциональна угловой скорости двигателя.
 Константа пропорциональности – это константа противо-ЭДС двигателя.
Константа пропорциональности – это константа противо-ЭДС двигателя.Где:
ω = угловая скорость двигателя
k E = постоянная противо-ЭДС двигателяСледовательно, путем замены:
Константа противо-ЭДС двигателя обычно указывается производителем двигателя в В/об/мин или мВ/об/мин. Чтобы получить осмысленное значение противо-ЭДС, необходимо указать скорость двигателя в единицах, совместимых с заданной константой противо-ЭДС.
«Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов».
(правило напряжения Кирхгофа)Постоянная двигателя зависит от конструкции катушки, силы и направления силовых линий в воздушном зазоре. Хотя можно показать, что обычно указанные три константы двигателя (константа противо-ЭДС, константа крутящего момента и константа скорости) равны, если используются соответствующие единицы измерения, расчет облегчается заданием трех констант в общепринятых единицах измерения.

Крутящий момент, создаваемый ротором, прямо пропорционален току в обмотках якоря. Константа пропорциональности – это константа крутящего момента двигателя.
Где:
M m = Крутящий момент, развиваемый двигателем
k M = Постоянный крутящий момент двигателяПодставляя это соотношение для текущих выходов:
Крутящий момент, развиваемый на роторе, равен моменту трения двигателя плюс момент нагрузки (из-за внешней механической нагрузки):
Где:
M R = Момент трения двигателя
M L = Момент нагрузкиЕсли предположить, что на клеммы двигателя подается постоянное напряжение, скорость двигателя будет прямо пропорциональна сумме момента трения и момента нагрузки.Константа пропорциональности представляет собой наклон кривой крутящий момент-скорость. Производительность двигателя лучше, когда этот наклон имеет меньшее значение.
 Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Этот коэффициент можно рассчитать по формуле:
Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Этот коэффициент можно рассчитать по формуле:где:
Δn = изменение скорости
Δm
ΔM = изменение крутящего момента
м ч = стойло крутящий момент
N 0 = без нагрузки скоростьАльтернативный подход к получению этого значение для скорости, n :
Используя исчисление, мы дифференцируем обе стороны относительно M , что дает:
Хотя мы не показываем отрицательный знак здесь, это подразумевается что результат даст снижение (отрицательный) склон.
Пример теоретического расчета двигателя
Давайте немного углубимся в теоретические расчеты.
 Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 .Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.
Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 .Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.Во-первых, давайте получим общее представление о работе двигателя, рассчитав постоянную двигателя k m . В этом случае мы получаем константу 28,48 мНм/А. «Согласно техпаспорту двигателя, электрическое сопротивление составляет 1,03 Ом в холодном состоянии для варианта 24 В».
Скорость двигателя под нагрузкой — это просто скорость холостого хода за вычетом снижения скорости из-за нагрузки.Константа пропорциональности для отношения между скоростью двигателя и крутящим моментом двигателя представляет собой наклон кривой зависимости крутящего момента от скорости, определяемый отношением скорости холостого хода двигателя к крутящему моменту двигателя.
 В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное нагрузкой крутящего момента 68 мНм, путем исключения единиц мНм:
В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное нагрузкой крутящего момента 68 мНм, путем исключения единиц мНм:Теперь через замену:
Тогда скорость двигателя под нагрузкой должна быть примерно:
Ток двигателя под нагрузкой представляет собой сумму тока холостого хода и тока под нагрузкой.
Константа пропорциональности, связывающая ток с нагрузкой крутящего момента, представляет собой константу крутящего момента ( k M ) .
 Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мНм, а ток, возникающий от этой нагрузки (без учета повышения температуры), приблизительно равен:
Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мНм, а ток, возникающий от этой нагрузки (без учета повышения температуры), приблизительно равен:Общий ток двигателя можно приблизительно определить путем суммирования этого значения с током двигателя без нагрузки.В техническом описании ток холостого хода двигателя указан как 78 мА. После округления общий ток примерно равен:
Выходная механическая мощность двигателя представляет собой просто произведение скорости двигателя и крутящего момента с поправочным коэффициентом для единиц измерения (если требуется). Следовательно, выходная мощность двигателя будет приблизительно равна:
Механическая мощность, потребляемая двигателем, представляет собой произведение приложенного напряжения и полного тока двигателя в амперах. В этом приложении:
Поскольку КПД η — это просто деление выходной мощности на входную мощность, давайте посчитаем его в нашей рабочей точке:
Оценка температуры обмотки двигателя во время работы:
Ток I , протекающий через сопротивление R , приводит к потере мощности в виде тепла I 2 · R .
 В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности в виде тепла в обмотках составляют:
В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности в виде тепла в обмотках составляют:Тепло, возникающее в результате I 2 · R потерь в катушке, рассеивается за счет теплопроводности через компоненты двигателя и поток воздуха в воздушном зазоре. Легкость, с которой это тепло может быть рассеяно в двигателе (или любой системе), определяется тепловым сопротивлением.
Термическое сопротивление (которое является обратной величиной теплопроводности) показывает, насколько хорошо материал сопротивляется передаче тепла по определенному пути. Производители двигателей обычно указывают способность двигателя рассеивать тепло, указывая значения теплового сопротивления R th . Например, алюминиевая пластина большого сечения будет иметь очень низкое тепловое сопротивление, в то время как значения для воздуха или вакуума будут значительно выше.
 В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Суммарные I 2 · R потери в катушке (источнике тепла) умножаются на термические сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется по формуле:
В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Суммарные I 2 · R потери в катушке (источнике тепла) умножаются на термические сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется по формуле:Где:
ΔT = Изменение температуры в К
I = Ток через обмотки двигателя в А
R = Сопротивление обмоток двигателя в Ом в К/Вт
R th3 = Термическое сопротивление корпуса к окружающей среде в К/ВтПродолжим наш пример, используя двигатель 2668W024CR, работающий с током 2458 А в обмотках двигателя, с сопротивлением якоря 1, 03 Ом, тепловое сопротивление между обмоткой и корпусом 3 К/Вт и тепловое сопротивление между корпусом и окружающей средой 8 К/Вт.
 Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :Поскольку шкала Кельвина использует тот же шаг единиц, что и шкала Цельсия, мы можем просто заменить значение Кельвина, как если бы оно было значением Цельсия. Если предположить, что температура окружающего воздуха составляет 22°C, то конечную температуру обмоток двигателя можно приблизительно представить как:
Где:
T теплый = Температура обмотки
Важно убедиться, что конечная температура обмоток не превышает номинальное значение двигателя, указанное в паспорте.В приведенном выше примере максимально допустимая температура обмотки составляет 125°C. Поскольку расчетная температура обмотки составляет всего 90,4°C, тепловое повреждение обмоток двигателя не должно быть проблемой в этом приложении.
Подобные расчеты можно было бы использовать для ответа на вопрос другого типа.
 Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C.Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Итак, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C.Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Итак, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°CТеперь мы можем рассчитать увеличение сопротивления катушки за счет рассеивания тепловой мощности:
Где:
α Cu = Температурный коэффициент меди в единицах K -1
(Обратные Кельвины)Так, из-за нагрева катушки и магнита за счет рассеивания мощности от потерь I 2 · R сопротивление катушки увеличилось с 1,03 Ом до 1,44 Ом.
 Теперь мы можем пересчитать новую константу крутящего момента k M , чтобы проследить влияние повышения температуры на производительность двигателя:
Теперь мы можем пересчитать новую константу крутящего момента k M , чтобы проследить влияние повышения температуры на производительность двигателя:Где:
α M = Температурный коэффициент магнита в единицах K -1
(обратные Кельвины)Теперь мы пересчитываем новую константу противо-ЭДС k E и наблюдаем за результатами. Из формулы, которую мы вывели выше:
Как мы видим, константа крутящего момента ослабевает в результате повышения температуры, как и константа противо-ЭДС! Таким образом, сопротивление обмотки двигателя, постоянная крутящего момента и постоянная противо-ЭДС оказывают негативное влияние по той простой причине, что они являются функциями температуры.
Мы могли бы продолжить расчет дополнительных параметров из-за более горячих катушки и магнита, но наилучшие результаты дает выполнение нескольких итераций, что лучше всего делать с помощью количественного программного обеспечения.
 Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту.Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (с использованием значений R и k M при температуре окружающей среды).
Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту.Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (с использованием значений R и k M при температуре окружающей среды).Обратите внимание, что максимально допустимый ток через обмотки двигателя можно увеличить, уменьшив тепловое сопротивление двигателя. Термическое сопротивление между ротором и корпусом R th2 в основном определяется конструкцией двигателя. Тепловое сопротивление корпуса к окружающей среде R th3 можно значительно уменьшить за счет добавления радиаторов.Термическое сопротивление двигателя для небольших двигателей постоянного тока обычно указывается для двигателя, подвешенного на открытом воздухе.
 Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление двигателя, установленного на металлической пластине известных размеров и материала.
Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление двигателя, установленного на металлической пластине известных размеров и материала.Для получения дополнительной информации о расчетах бессердечных щеточных двигателей постоянного тока и о том, как рассеивание тепловой мощности может повлиять на характеристики электродвигателя, обратитесь к квалифицированному инженеру по применению FAULHABER.Мы всегда готовы помочь.
Индуктивность якоря – обзор
Как уже указывалось, установившийся ток якоря зависит от небольшой разницы между противоэ.д.с. E и приложенное напряжение V . В приводе с питанием от преобразователя жизненно важно, чтобы ток оставался в безопасных пределах, иначе тиристоры или транзисторы (которые имеют очень ограниченную перегрузочную способность по току) будут разрушены, и это следует из уравнения.
 (3.8) что для предотвращения превышения током его номинального значения мы не можем допустить, чтобы В и Е отличались более чем на IR , где I — номинальный ток.
(3.8) что для предотвращения превышения током его номинального значения мы не можем допустить, чтобы В и Е отличались более чем на IR , где I — номинальный ток.Было бы неприемлемо, например, пытаться привести все, кроме наименьшего постоянного тока. разгонять двигатели до скорости простым включением номинального напряжения. В рассмотренном ранее примере номинальное напряжение составляет 500 В, а сопротивление якоря — 1 Ом. В состоянии покоя противоэдс равен нулю, и, следовательно, начальный ток будет 500/1 = 500 А, или в 25 раз больше номинального тока! Это приведет к выходу из строя тиристоров в преобразователе питания (и/или перегоранию предохранителей). Очевидно, что начальное напряжение, которое мы должны применить, намного меньше 500 В; и если мы хотим ограничить ток до номинального значения (20 А в примере), необходимое напряжение будет 20 × 1, т.е.е. всего 20 вольт. По мере увеличения скорости противо-Э.Д.С. повышается, и для поддержания полного тока напряжение V также должно увеличиваться таким образом, чтобы разница между V и E оставалась постоянной на уровне 20 В.
 Конечно, при контроле тока двигатель не будет разгоняться так быстро, как если бы мы включили полное напряжение и позволили току делать то, что ему хотелось. Но это цена, которую мы должны заплатить, чтобы защитить преобразователь.
Конечно, при контроле тока двигатель не будет разгоняться так быстро, как если бы мы включили полное напряжение и позволили току делать то, что ему хотелось. Но это цена, которую мы должны заплатить, чтобы защитить преобразователь.Аналогичные проблемы со скачками тока возникают, если нагрузка на двигатель резко увеличивается, так как это приводит к замедлению двигателя с последующим падением E.В каком-то смысле мы приветствуем падение E, потому что это приводит к увеличению тока, необходимого для питания дополнительной нагрузки, но, конечно, мы хотим, чтобы ток возрастал только до своего номинального значения: за пределами этой точки мы должны быть готовы уменьшить V, чтобы предотвратить чрезмерный ток.
Решение проблемы перегрузок по току заключается в обеспечении ограничения тока с обратной связью как неотъемлемой функции двигателя/привода. Ток двигателя измеряется, и напряжение В автоматически регулируется таким образом, чтобы номинальный ток не превышался постоянно, хотя обычно он может достигать 1.
 5-кратный номинальный ток на срок до 60 с. Мы обсудим текущий контур управления в главе 4.
5-кратный номинальный ток на срок до 60 с. Мы обсудим текущий контур управления в главе 4.3.5.1 Динамическое поведение и временные константы
Использование терминов «всплеск» и «внезапный» в приведенном выше обсуждении, несомненно, создаст впечатление, что изменения в ток или скорость двигателя могут изменяться мгновенно, тогда как на самом деле всегда требуется конечное время, чтобы произвести изменения в любом из них. (Если изменяется ток, то изменяется и энергия, запасенная в индуктивности якоря, а если изменяется скорость, изменяется кинетическая энергия вращения, запасенная в инерции.Чтобы любое из этих изменений произошло в нулевое время, необходим был бы импульс бесконечной мощности, что, очевидно, невозможно.)
Теоретическое рассмотрение переходной динамики постоянного тока. машина проще, чем для любого другого типа электродвигателя, но, тем не менее, выходит за рамки нашей компетенции. Однако стоит обобщить основные черты динамического поведения и подчеркнуть тот факт, что все происходящие переходные изменения определяются только двумя постоянными времени.
 Первый (и наиболее важный с точки зрения пользователя) — это электромеханическая постоянная времени, которая определяет, как скорость устанавливается на новый уровень после возмущения, такого как изменение напряжения якоря или момента нагрузки. Вторая — электрическая (или якорная) постоянная времени, которая обычно намного короче и определяет скорость изменения тока якоря сразу после изменения напряжения якоря.
Первый (и наиболее важный с точки зрения пользователя) — это электромеханическая постоянная времени, которая определяет, как скорость устанавливается на новый уровень после возмущения, такого как изменение напряжения якоря или момента нагрузки. Вторая — электрическая (или якорная) постоянная времени, которая обычно намного короче и определяет скорость изменения тока якоря сразу после изменения напряжения якоря.Когда двигатель работает, есть два «входа», которые мы можем внезапно изменить, а именно приложенное напряжение и крутящий момент нагрузки.При изменении любого из них двигатель входит в переходный период, прежде чем перейти в новое устойчивое состояние. Оказывается, что если пренебречь индуктивностью якоря (т.е. принять постоянную времени якоря равной нулю), переходный период характеризуется экспоненциальными характеристиками первого порядка по скорости и току. Это предположение справедливо для всех двигателей, кроме самых больших. Аналогичный результат мы получили, когда рассматривали примитивный линейный двигатель в главе 1 (см.
 рис. 1.16).
рис. 1.16).Например, если мы резко увеличим напряжение якоря двигателя без трения и без нагрузки с В 1 до В 2 , его скорость и ток изменятся, как показано на рис.3.11.
Рис. 3.11. Ответ постоянного тока двигатель для ступенчатого увеличения напряжения якоря.
Происходит немедленное увеличение тока (поскольку мы проигнорировали индуктивность), отражающее тот факт, что приложенное напряжение внезапно превышает противоэдс; увеличенный ток создает больший крутящий момент и, следовательно, двигатель ускоряется; рост скорости сопровождается увеличением противоЭДС, поэтому ток начинает падать; и процесс продолжается до тех пор, пока не будет достигнута новая установившаяся скорость, соответствующая новому напряжению.В этом конкретном случае установившийся ток равен нулю, потому что мы предположили, что нет трения или момента нагрузки, но форма динамического отклика была бы такой же, если бы была начальная нагрузка или если бы мы внезапно изменили нагрузка.

Выражение, описывающее ток как функцию времени ( t ):
(3.11)i=V2−V1Re−tτ
экспоненциальный переходный член, e−tτ.Значение постоянной времени ( τ ) показано на рис. 3.11. Если проецируется начальный градиент графика текущего времени, он пересекает конечное значение через одну постоянную времени. Теоретически для установления отклика требуется бесконечное время, но на практике переходный процесс обычно считается завершенным примерно через 4 или 5 постоянных времени. Мы отмечаем, что переходная характеристика очень удовлетворительна: как только напряжение увеличивается, ток сразу же увеличивается, чтобы обеспечить больший крутящий момент и начать ускорение, но ускоряющий крутящий момент постепенно уменьшается, чтобы обеспечить плавное приближение к новой целевой скорости.К счастью, поскольку система является системой первого порядка, нет намека на колебательный отклик с выбросами.
Анализ дает взаимосвязь между постоянной времени и параметрами двигателя/системы как
(3.
 12)τ=RJk2
12)τ=RJk2, где R — сопротивление якоря, Дж — общая инерция вращения двигателя плюс нагрузка, а k — постоянная двигателя (уравнения 3.3 и 3.4). Уместность термина «электромеханическая постоянная времени» должна быть ясна из уравнения(3.12), поскольку τ зависит от электрических параметров ( R и k ) и механического параметра, Дж. в два раза дольше, возможно, следует ожидать, но влияние параметров двигателя R и k , вероятно, не столь очевидно.
Электрическая постоянная времени или постоянная времени якоря определяется обычным способом для цепей серий L , R , т.е.е.
(3.13)τa=LR
при остановленном двигателе и подаче на якорь ступенчатого напряжения В ток экспоненциально возрастает до конечного значения В/об с постоянной времени τ a .
Если бы мы всегда применяли чистый постоянный ток. напряжение на двигатель, вероятно, хотелось бы, чтобы τ a было как можно короче, чтобы не было задержки нарастания тока при изменении напряжения.

Но, учитывая, что большинство двигателей питаются от волн напряжения, которые далеки от гладких (см. главу 2), мы на самом деле довольно рады обнаружить, что из-за индуктивности и связанной с ней постоянной времени форма волны тока (и, следовательно, крутящий момент) имеют более гладкую форму, чем форма сигнала напряжения. Таким образом, неизбежное присутствие индуктивности якоря оказывается (в большинстве случаев) скрытым благом.
До сих пор мы смотрели на две постоянные времени так, как будто они не связаны друг с другом по влиянию, которое они оказывают на ток.Мы начали с электромеханической постоянной времени, предполагая, что постоянная времени якоря равна нулю, и увидели, что доминирующее влияние на ток во время переходного процесса оказывает ЭДС движения. Затем мы исследовали ток, когда ротор был неподвижен (так что ЭДС движения равна нулю), и увидели, что рост или спад тока определяется индуктивностью якоря, проявляющейся через постоянную времени якоря.
В действительности обе постоянные времени влияют на ток одновременно, и картина оказывается более сложной, чем мы предполагали, так как система на самом деле является системой второго порядка.
 Однако хорошая новость заключается в том, что для большинства двигателей и большинства целей мы можем воспользоваться тем фактом, что постоянная времени якоря намного короче, чем электромеханическая постоянная времени. Это позволяет нам аппроксимировать поведение, отделив относительно быстрые «электрические переходные процессы» в цепи якоря от гораздо более медленных «электромеханических переходных процессов», которые видны пользователю. С точки зрения последнего интерес, вероятно, представляет только электромеханический переходный процесс.
Однако хорошая новость заключается в том, что для большинства двигателей и большинства целей мы можем воспользоваться тем фактом, что постоянная времени якоря намного короче, чем электромеханическая постоянная времени. Это позволяет нам аппроксимировать поведение, отделив относительно быстрые «электрические переходные процессы» в цепи якоря от гораздо более медленных «электромеханических переходных процессов», которые видны пользователю. С точки зрения последнего интерес, вероятно, представляет только электромеханический переходный процесс.Частоты и генераторы переменного тока. Тригонометрия и генерация однофазного переменного тока для электриков
В предыдущей главе мы узнали, что термин цикл означает от точки сигнала до точки, в которой сигнал начинает повторяться.Когда мы обсуждаем термин частота , мы имеем в виду, сколько циклов может произойти в одну секунду. Частота измеряется в герц (восклицаем Генриху Герцу) или герц (циклов в секунду).
Рисунок 52. Цикл синусоиды На частоту генератора влияют два фактора: скорость вращения и количество полюсов.
На частоту генератора влияют два фактора: скорость вращения и количество полюсов.Когда якорь вращается в поле, он начинает создавать форму волны (как мы видели в предыдущей главе). Один полный механический оборот якоря создает одну полную синусоиду на двухполюсном генераторе переменного тока.Если двухполюсный генератор делает три полных оборота за одну секунду, он создаст за эту секунду три полных синусоидальных колебания. Мы бы сказали, что частота составляет три цикла в секунду или три герца (как говорят крутые ребята).
Скорость вращения машины измеряется в оборотах в минуту или об/мин . Однако при работе с частотой нас интересуют не минуты, а скорее секунды. Следовательно, RPM необходимо преобразовать в обороты в секунду ( RPS ).Поскольку в минуте 60 секунд, все, что нам нужно сделать, это разделить RPM на 60, чтобы преобразовать его в RPS.
Например, если якорь двухполюсного генератора переменного тока вращается со скоростью 1800 об/мин, мы можем сказать, что он вращается со скоростью 30 оборотов в секунду.
 Если этот генератор переменного тока имеет два полюса, то за одну секунду он будет генерировать 30 циклов напряжения. Тогда можно было бы сказать, что он имеет частоту 30 циклов в секунду или 30 герц. Частота генератора прямо пропорциональна скорости вращения генератора.
Если этот генератор переменного тока имеет два полюса, то за одну секунду он будет генерировать 30 циклов напряжения. Тогда можно было бы сказать, что он имеет частоту 30 циклов в секунду или 30 герц. Частота генератора прямо пропорциональна скорости вращения генератора.Если мы добавим полюса к генератору, мы сможем изменить частоту. В двухполюсном генераторе переменного тока сторона А якоря (показанная на рис. 53) проходит с севера на юг, а затем с юга на север, создавая одну полную синусоиду. Если мы добавим еще два полюса, как показано на рис. 54, то сторона А якоря пройдет мимо двух северных и двух южных полюсов за один полный механический оборот.
Рис. 53. Двухполюсный генератор переменного токаДве полные синусоидальные волны создаются за один полный механический оборот.Если двухполюсный генератор создает один цикл напряжения за одну секунду (или один герц частоты), то четырехполюсный генератор создает два цикла напряжения за одну секунду (или два герца).

Частота генератора прямо пропорциональна количеству полюсов генератора.
Рисунок 54. Четырехполюсный генераторЗная, что скорость вращения прямо пропорциональна частоте и что количество полюсов прямо пропорционально частоте, мы можем использовать формулу.Формула выглядит так:
Рисунок 55. Формула частотыГде…
f = частота в герцах
P = количество полюсов
N = скорость вращения в об/мин
Мы делим количество полюсов на два, потому что всегда будет набор из двух полюсов. У вас не может быть северного полюса без юга. Мы делим число оборотов в минуту на 60, потому что нас интересуют обороты в секунду, а не обороты в минуту. Формулу на рис. 56 можно комбинировать, чтобы она выглядела так:
.
Рисунок 56.Комбинированная частотная формулаВ этом видео показано, как частота связана с числом оборотов в минуту и числом полюсов генератора переменного тока.



 Для того, чтобы придать бетонной отливке прочность и устойчивость к воздействию по любым направлениям – в тело бетонной отливки внедряется металлический силовой каркас.
Для того, чтобы придать бетонной отливке прочность и устойчивость к воздействию по любым направлениям – в тело бетонной отливки внедряется металлический силовой каркас.
 В этом случае необходимо рассчитывать ее вес индивидуально, с применением специальных формул. Хорошим решением будет использование для такого расчета математических электронных таблиц.
В этом случае необходимо рассчитывать ее вес индивидуально, с применением специальных формул. Хорошим решением будет использование для такого расчета математических электронных таблиц.




 Следовательно
Следовательно 25А\)
25А\) Вы можете сравнить максимальный основной коэффициент обмотки для различных комбинаций количества полюсов и количества пазов, отобразить схему обмотки для различных пролетов катушек или оценить спектр гармоник коэффициента обмотки.
Вы можете сравнить максимальный основной коэффициент обмотки для различных комбинаций количества полюсов и количества пазов, отобразить схему обмотки для различных пролетов катушек или оценить спектр гармоник коэффициента обмотки.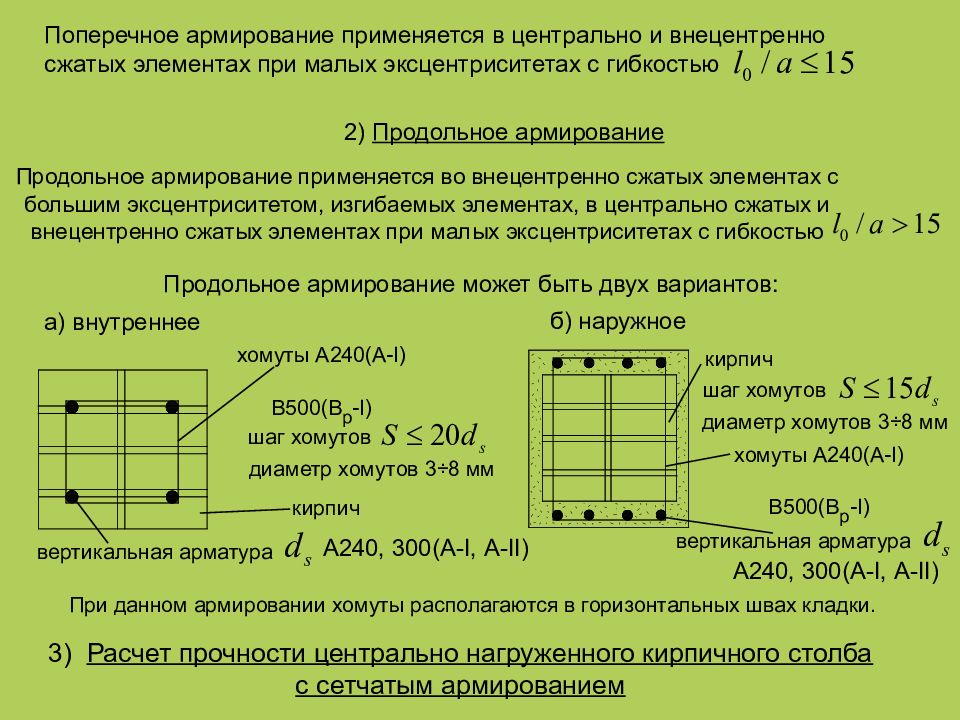
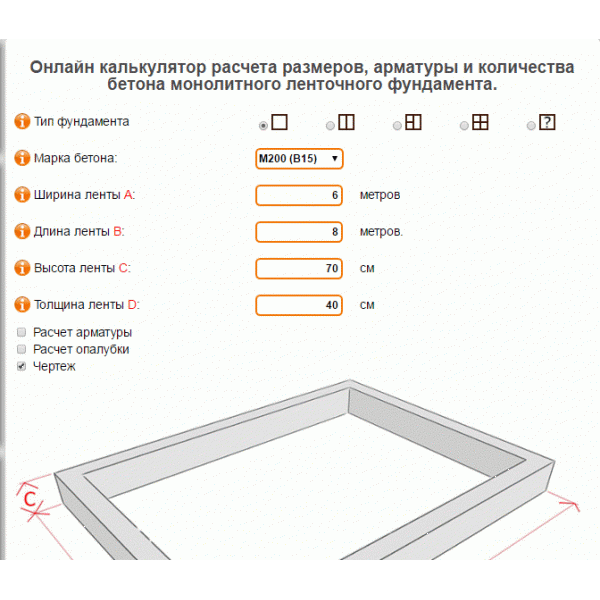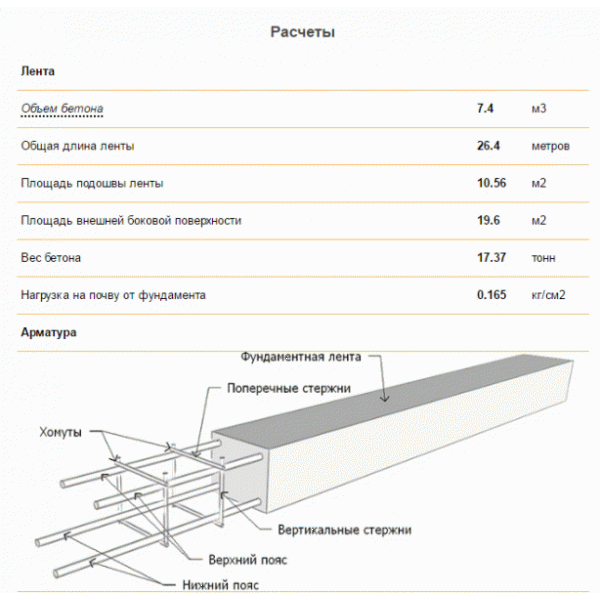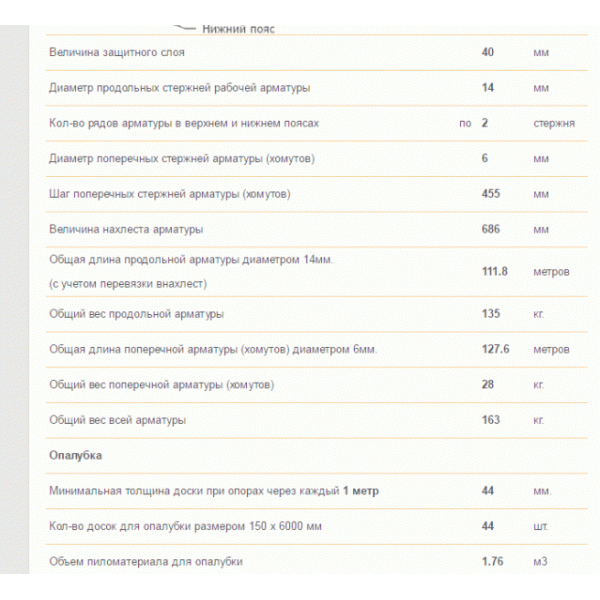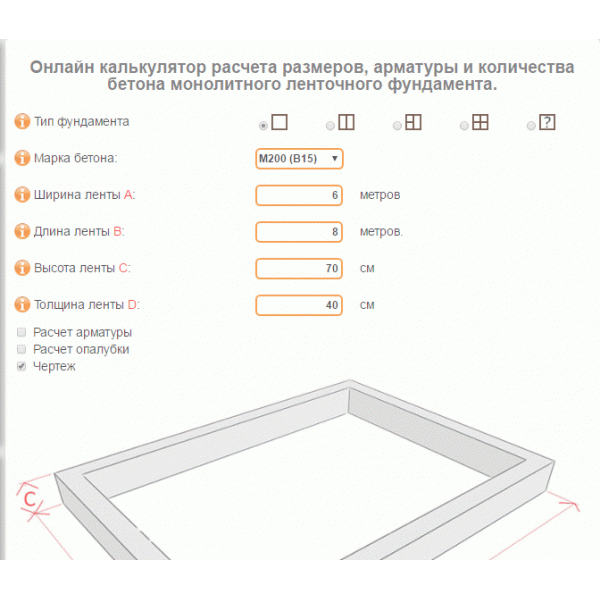
 д.
д.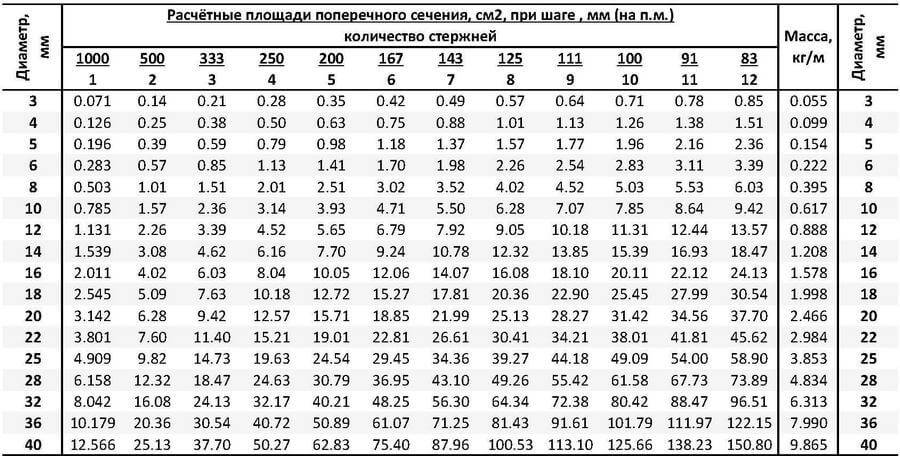
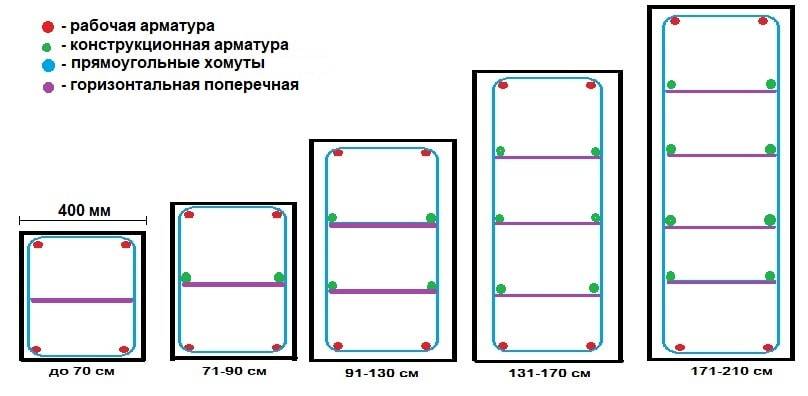
 В то время как потери в сердечнике, такие как гистерезис и потери на вихревые токи, механические потери, такие как потери на трение, являются постоянными потерями.
В то время как потери в сердечнике, такие как гистерезис и потери на вихревые токи, механические потери, такие как потери на трение, являются постоянными потерями.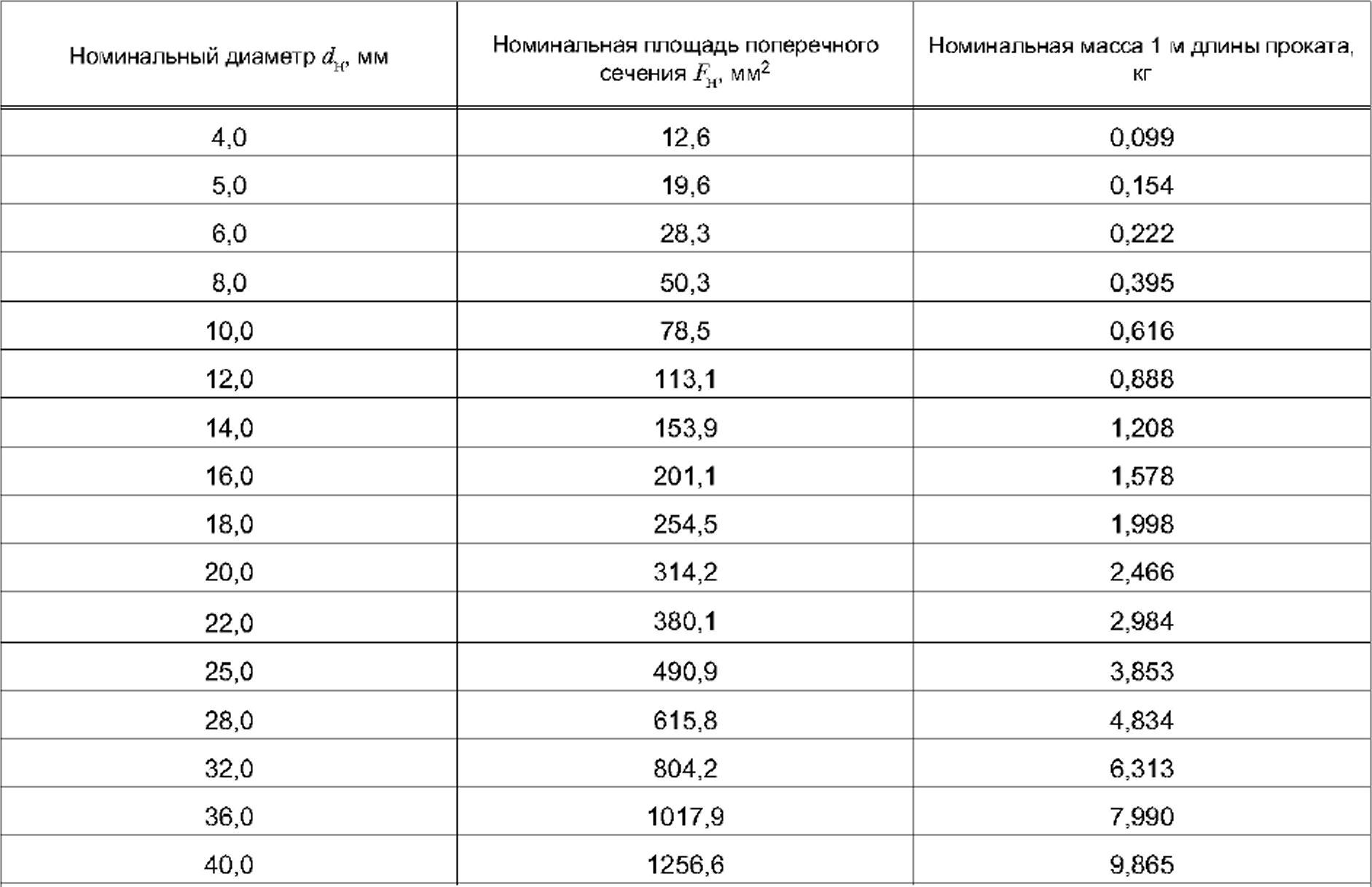

 Это достигается путем умножения скорости на коэффициент преобразования единиц 2π/60 . Кроме того, если « M » (крутящий момент) выражается в мНм , то мы должны умножить его на 10 -3 (разделить на 1 000), чтобы преобразовать единицы измерения в Нм для целей расчета.
Это достигается путем умножения скорости на коэффициент преобразования единиц 2π/60 . Кроме того, если « M » (крутящий момент) выражается в мНм , то мы должны умножить его на 10 -3 (разделить на 1 000), чтобы преобразовать единицы измерения в Нм для целей расчета.
 Если у вас есть несколько основных единиц лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.
Если у вас есть несколько основных единиц лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке. Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем.Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.
Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем.Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка. Затем вращайте вал двигателя
и сделайте еще одно измерение. Измерения
должны быть очень близки по значению. Продолжайте вращать вал
и сделайте не менее трех измерений. Это обеспечит
что измерения проводились не в точке
минимальный контакт на коммутаторе.
Затем вращайте вал двигателя
и сделайте еще одно измерение. Измерения
должны быть очень близки по значению. Продолжайте вращать вал
и сделайте не менее трех измерений. Это обеспечит
что измерения проводились не в точке
минимальный контакт на коммутаторе. Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.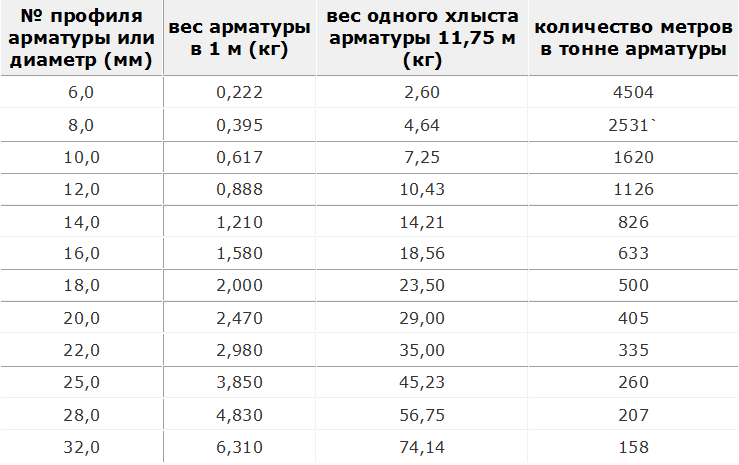 Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.
Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента. В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность.Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.
В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность.Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.
Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики. Из-за нехватки места отображается пример расчета для одной точки.
Из-за нехватки места отображается пример расчета для одной точки.
 Константа пропорциональности – это константа противо-ЭДС двигателя.
Константа пропорциональности – это константа противо-ЭДС двигателя.
 Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Этот коэффициент можно рассчитать по формуле:
Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Этот коэффициент можно рассчитать по формуле: Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 .Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.
Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 .Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости. В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное нагрузкой крутящего момента 68 мНм, путем исключения единиц мНм:
В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное нагрузкой крутящего момента 68 мНм, путем исключения единиц мНм: Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мНм, а ток, возникающий от этой нагрузки (без учета повышения температуры), приблизительно равен:
Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мНм, а ток, возникающий от этой нагрузки (без учета повышения температуры), приблизительно равен: В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности в виде тепла в обмотках составляют:
В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности в виде тепла в обмотках составляют: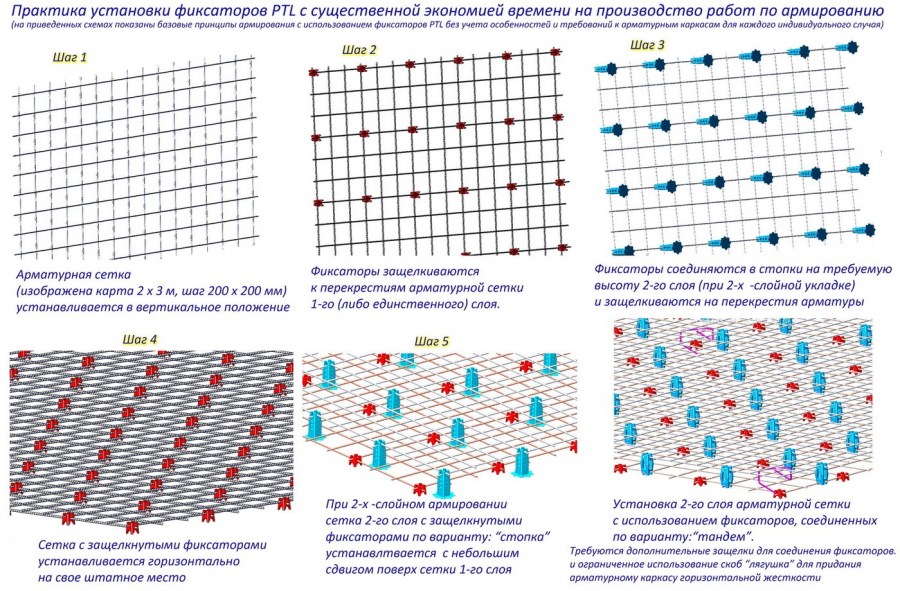 В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Суммарные I 2 · R потери в катушке (источнике тепла) умножаются на термические сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется по формуле:
В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Суммарные I 2 · R потери в катушке (источнике тепла) умножаются на термические сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется по формуле: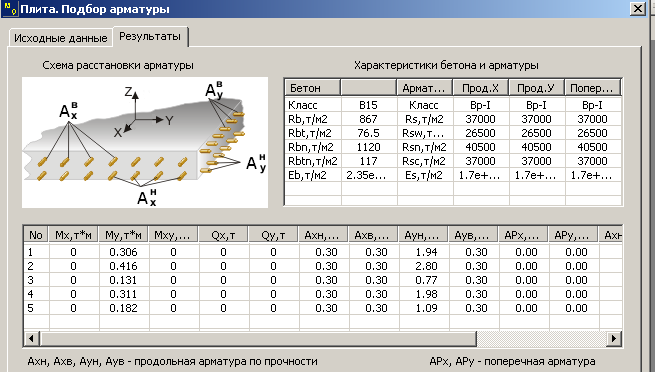 Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R : Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C.Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Итак, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C.Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Итак, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C Теперь мы можем пересчитать новую константу крутящего момента k M , чтобы проследить влияние повышения температуры на производительность двигателя:
Теперь мы можем пересчитать новую константу крутящего момента k M , чтобы проследить влияние повышения температуры на производительность двигателя: Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту.Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (с использованием значений R и k M при температуре окружающей среды).
Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту.Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (с использованием значений R и k M при температуре окружающей среды). Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление двигателя, установленного на металлической пластине известных размеров и материала.
Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление двигателя, установленного на металлической пластине известных размеров и материала.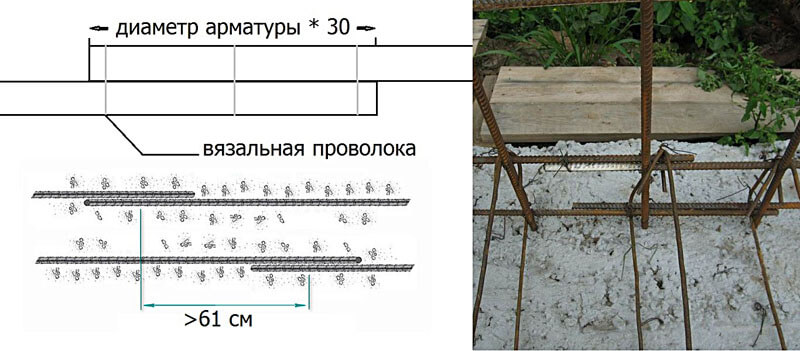 (3.8) что для предотвращения превышения током его номинального значения мы не можем допустить, чтобы В и Е отличались более чем на IR , где I — номинальный ток.
(3.8) что для предотвращения превышения током его номинального значения мы не можем допустить, чтобы В и Е отличались более чем на IR , где I — номинальный ток. Конечно, при контроле тока двигатель не будет разгоняться так быстро, как если бы мы включили полное напряжение и позволили току делать то, что ему хотелось. Но это цена, которую мы должны заплатить, чтобы защитить преобразователь.
Конечно, при контроле тока двигатель не будет разгоняться так быстро, как если бы мы включили полное напряжение и позволили току делать то, что ему хотелось. Но это цена, которую мы должны заплатить, чтобы защитить преобразователь.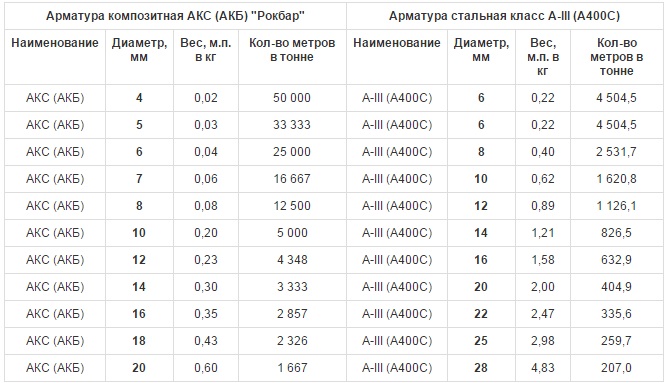 5-кратный номинальный ток на срок до 60 с. Мы обсудим текущий контур управления в главе 4.
5-кратный номинальный ток на срок до 60 с. Мы обсудим текущий контур управления в главе 4. Первый (и наиболее важный с точки зрения пользователя) — это электромеханическая постоянная времени, которая определяет, как скорость устанавливается на новый уровень после возмущения, такого как изменение напряжения якоря или момента нагрузки. Вторая — электрическая (или якорная) постоянная времени, которая обычно намного короче и определяет скорость изменения тока якоря сразу после изменения напряжения якоря.
Первый (и наиболее важный с точки зрения пользователя) — это электромеханическая постоянная времени, которая определяет, как скорость устанавливается на новый уровень после возмущения, такого как изменение напряжения якоря или момента нагрузки. Вторая — электрическая (или якорная) постоянная времени, которая обычно намного короче и определяет скорость изменения тока якоря сразу после изменения напряжения якоря. рис. 1.16).
рис. 1.16).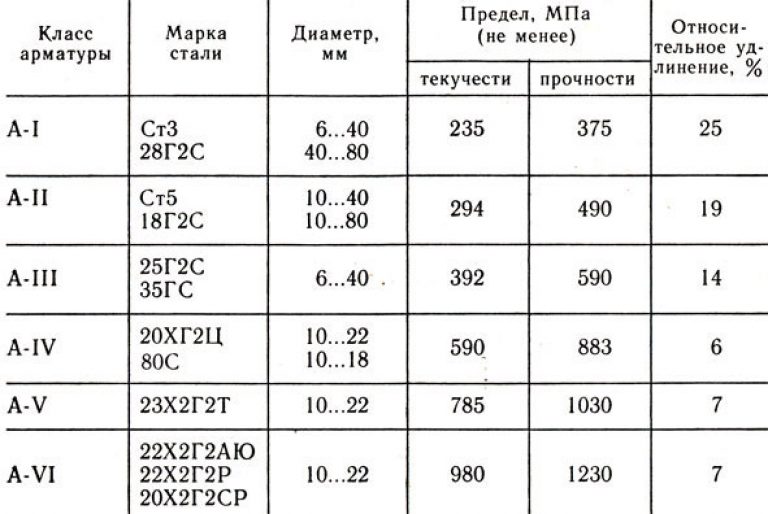

 Однако хорошая новость заключается в том, что для большинства двигателей и большинства целей мы можем воспользоваться тем фактом, что постоянная времени якоря намного короче, чем электромеханическая постоянная времени. Это позволяет нам аппроксимировать поведение, отделив относительно быстрые «электрические переходные процессы» в цепи якоря от гораздо более медленных «электромеханических переходных процессов», которые видны пользователю. С точки зрения последнего интерес, вероятно, представляет только электромеханический переходный процесс.
Однако хорошая новость заключается в том, что для большинства двигателей и большинства целей мы можем воспользоваться тем фактом, что постоянная времени якоря намного короче, чем электромеханическая постоянная времени. Это позволяет нам аппроксимировать поведение, отделив относительно быстрые «электрические переходные процессы» в цепи якоря от гораздо более медленных «электромеханических переходных процессов», которые видны пользователю. С точки зрения последнего интерес, вероятно, представляет только электромеханический переходный процесс. На частоту генератора влияют два фактора: скорость вращения и количество полюсов.
На частоту генератора влияют два фактора: скорость вращения и количество полюсов.
