Арматура распределительная: АРМАТУРА РАСПРЕДЕЛИТЕЛЬНАЯ | это… Что такое АРМАТУРА РАСПРЕДЕЛИТЕЛЬНАЯ?

Распределительно-смесительная арматура

Распределительно-смесительная арматура АРМАТЭК

Трубопроводная арматура, устанавливаемая на трубопроводах, оборудовании и различных емкостях, управляет потоком рабочей среды посредством изменения проходного сечения. Слово «управление» объединяет шесть функций трубопроводной арматуры — открытие, перекрытие, разделение, регулирование, распределение и смешивание. За два последних отвечает ее вид, носящий название распределительно-смесительная арматура.

Распределительно-смесительная арматура:

• распределяет поток рабочей среды по двум и более направлениям;
• смешивает потоки рабочей среды.

Самый наглядный пример ее работы, — перемешивая горячую и холодную воду, обеспечивать получение требуемой температуры потока.

О терминологии в трубопроводной арматуре

Определение распределительно-смесительной арматуры в нормативных документах за прошедшие более чем три десятилетия фактически не претерпело никаких изменений. Хотя некоторые нюансы есть. Если в «ГОСТ 24856-81. Арматура трубопроводная промышленная. Термины и определения» применение по отдельности частей сложного прилагательного «распределительно-смесительная» — распределительная или смесительная арматура — никак не комментировалось, то «Стандарт ЦКБА 011-2004. Арматура трубопроводная. Термины и определения» и «ГОСТ Р 52720-2007. Арматура трубопроводная. Термины и определения» их использование в таком виде не рекомендуют (или не рекомендовали, поскольку ГОСТ Р 52720-2007 уже официально отменен). В действующем сегодня «ГОСТ 24856-2014. Арматура трубопроводная. Термины и определения» применение терминов «распределительная арматура» — для арматуры, предназначенной только для распределения, и «смесительная арматура» — для арматуры, предназначенной только для смешивания потоков рабочей среды, считается возможным.

Во всех нормативных документах, регулирующих терминологию в трубопроводной арматуре, сказано о таких разновидностях распределительно-смесительной арматуры, как разделительный и смесительный клапаны.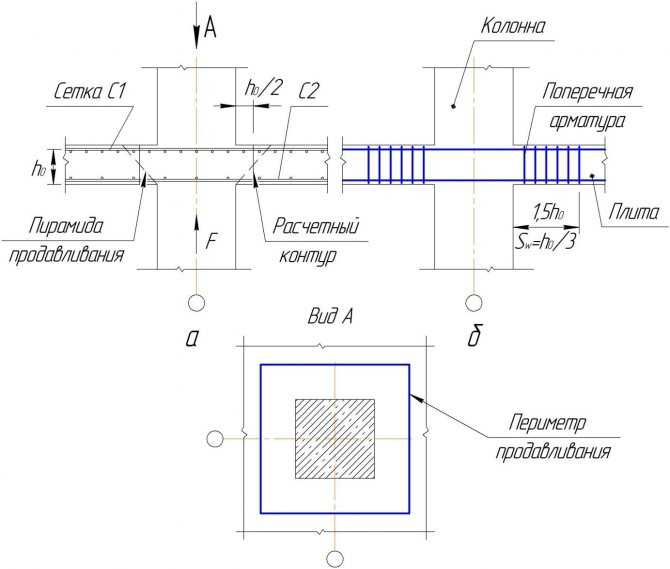 А в ГОСТ 24856-81 — еще и о распределительном кране. Интересно, что в этом же ГОСТ смесительный клапан назван регулирующим клапаном, что скорее прямо, чем косвенно, должно было свидетельствовать о его принадлежности к регулирующей арматуре. В ГОСТ 24856-2014 прилагательного «регулирующий» в формулировке определения смесительного клапана нет, зато одна из его глав называется «Разновидности регулирующей и распределительно-смесительной арматуры», что лишний раз подтверждает функциональную близость этих видов трубопроводной арматуры. Во многих классификациях смесительная арматура рассматривается как обладающая определенными особенностями «ветвь» регулирующей арматуры.

В рекламных буклетах и прайс-листах ряда компаний — производителей и поставщиков трубопроводной арматуры, можно встретить не установленные в нормативных документах термины «запорно-распределительная арматура» и запорно-смесительная арматура.

Слово «арматура» широко употребляется не только в терминологии, относящейся к трубопроводной арматуре, но и в других областях техники и технологий, например, в производстве железобетонных конструкций. Там используются монтажная, рабочая и распределительная арматура. (Еще одно название распределительной арматуры — конструктивная). Поэтому такие выражения, как «минимальный диаметр распределительной арматуры в плитах» или «распределительная арматура служит для равномерного распределения нагрузок», при всем своем внешнем сходстве с терминологией принятой в арматуростроении, не имеют к ней никакого отношения.

Многоходовая арматура

Среди разновидностей трубопроводной арматуры по конструкции и формообразованию корпуса в нормативах выделена т. н. многоходовая арматура. Это название носит распределительно-смесительная арматура, с суммарным числом патрубков три и более. Одновременно или попеременно рабочая среда входит и выходит в один или несколько из них. Например, в трехходовой арматуре возможны следующие варианты движения рабочей среды:

• рабочая среда входит в два патрубка, выходит в один — процесс смешивания;
• входит в один патрубок, а выходит в два — процесс распределения;
• входя в один патрубок, попеременно выходит в один из двух других.

Изготавливаются также четырехходовые, пятиходовые и содержащие в своем определении еще бо́льшие значения числительного клапаны и краны. Такие многоходовые устройства используются в различной аппаратуре: газовых дозаторах, устройствах для отбора проб (например, воздуха), различном лабораторном и промышленном оборудовании, для отбора или подачи теплоносителя из разных температурных слоев в накопительных водонагревателях и т. д.

Смесительные клапаны

Так называются клапаны, чье назначение — смешивать потоки двух и более рабочих сред, различных по параметрам и (или) свойствам.

Смесительные клапаны широко используют в коммунальной сфере — в общественных и жилых зданиях при устройстве приточной вентиляции, водоснабжения, теплоснабжения. Их устанавливают в котельных, местных и центральных тепловых пунктах.

Применение много ходовых смесительных клапанов в системах отопления, позволяет организовать раздельные регулируемые контуры, способные защитить отопительные котлы от низкотемпературной коррозии. Смесительные клапаны помогают обеспечивать стабильные параметры работы особенно популярных сегодня комфортных и энергосберегающих систем низкотемпературного отопления, таких как теплые водяные полы и встроенное настенное отопление.

Автоматическое поддержание с высокой точностью (до десятых долей градуса Цельсия) требуемой температуры за счет смешивания в нужных пропорциях высоко- и низкотемпературной составляющих потока теплоносителя, делают возможным термостатические смесительные клапаны. Рабочей средой может быть не только вода, но и другие жидкости и газы, не оказывающие на такой клапан ярко выраженного коррозионного воздействия. Управлять его работой можно с помощью термостатической головки — регулятора прямого действия, или сервопривода — исполнительного механизма дистанционного управления, получающего команду от управляющего устройства, например, от контроллера.

Термостатические смесительные клапаны используются также для предотвращения ожогов у пользователей систем горячего водоснабжения.

Температура — не единственный параметр, которым управляют, смешивая потоки рабочей среды. Можно добиваться требуемой плотности потока, например, его разжижения.

Распределительные клапаны

Распределительные клапаны, направляя рабочую среду в один из нескольких трубопроводов, служат для эффективного перераспределения потока по определенным направлениям.

Распределительные клапаны могут быть однопозиционными и двухпозиционными, прямого и непрямого действия.

Трехходовые и четырехходовые распределительные клапаны используют для управления пневмо- и гидроприводами, соответственно, — одностороннего и двухстороннего действия. Широкое распространение получили распределительные клапаны с электромагнитным приводом (иногда их называют соленоидные клапаны), осуществляющие автоматическое и дистанционное с помощью пульта управление гидравлическими и пневматическими приводами трубопроводной арматуры, установленной на объектах электроэнергетики и других отраслей промышленности. В частности, в нефтегазовой отрасли, где распределительные клапаны являются компонентами систем управления устьевым оборудованием. Управление распределительными электромагнитными клапанами осуществляется с помощью одного или двух электромагнитов. В зависимости от вида воздействия на исполнительный механизм различают тянущие и толкающие электромагниты.

Фиксация положения золотника в распределительном клапане может происходить за счет усилий создаваемых давлением рабочей среды, постоянной подачи тока в обмотки электромагнита или с помощью механического фиксатора (защелки).

Режимы работы электромагнита (-ов) распределительного клапана бывают длительными и кратковременными. Например, на промышленных гидравлических прессах устанавливают распределительные клапаны, срабатывающие одновременно с включением электромагнита. Как только электромагнит выключается, перестает работать распределительный клапан.

Распределительные краны

Для перераспределения потоков рабочей среды по нескольким направлениям могут использоваться распределительные краны. Их применяют для регулирования теплоотдачи отопительных приборов, в теплых полах и горячем водоснабжении (ГВС).

Наглядными примерами сантехнической распределительно-смесительной арматуры является трехходовой кран, служащий для регулирования теплоотдачи отопительных приборов, или распределительный кран, от положения ручки которого, зависит, куда направится поток воды, — наполнять ванну или в шланг для душа.

С помощью распределительных кранов управляют движением сжатого воздуха в пневмосистемах, в частности, работой пневмодвигателей. Их устанавливают в гидравлических системах для регулирования работы, входящих в их состав гидравлических устройств.

Распределительно-смесительная арматура — универсальное оборудование. Используя смесительные и распределительные клапаны, а также распределительные краны, можно эффективно управлять самыми разными рабочими средами: водой и водными растворами, паром, нефтью, нефтепродуктами, природным газом, азотом, кислородом, углекислым газом и т. д.

Для изготовления распределительно-смесительной арматуры используют широкий спектр конструкционных материалов: все виды сталей — углеродистую, легированную, нержавеющую, а также чугун, латунь, титан.

Применяются все возможные способы присоединения к трубопроводу: муфтовое, под приварку, фланцевое, цапковое, штуцерное.

Такое разнообразие материалов и конструкций обеспечивают огромные функциональные возможности распределительно-смесительной арматуры.

Интересная особенность — среди всех основных видов трубопроводной арматуры распределительно-смесительная арматура единственная, содержит в своем наименовании сложное, написанное через дефис, прилагательное. Любые другие, в чьем названии присутствует этот небуквенный орфографический знак, относятся к комбинированной арматуре (запорно-регулирующая, запорно-обратная и т. д.). Несмотря на почти полную противоположность процессов смешивания и распределения, их выполнение обеспечивают конструктивно и функционально близкие между собой технические устройства. Настолько близкие, что в процессе классификации их даже не потребовалось разносить по разным тематическим «ячейкам», ограничившись одним видом, носящим название распределительно-смесительная арматура.

рабочая распределительная монтажная арматура хомуты

Как указывалось ранее, в качестве арматуры употребляют главным образом круглую сталь и сталь периодического профиля в виде отдельных прутков диаметром до 40 мм, а также сваренную или связанную в арматурные каркасы.

Для элементов массивных железобетонных гидротехнических сооружений, например шлюзов, имеющих большие размеры сечений, целесообразно применять стержни крупных диаметров до 90—120 мм. Кроме круглой стали, в качестве арматуры применяют сталь и других профилей.

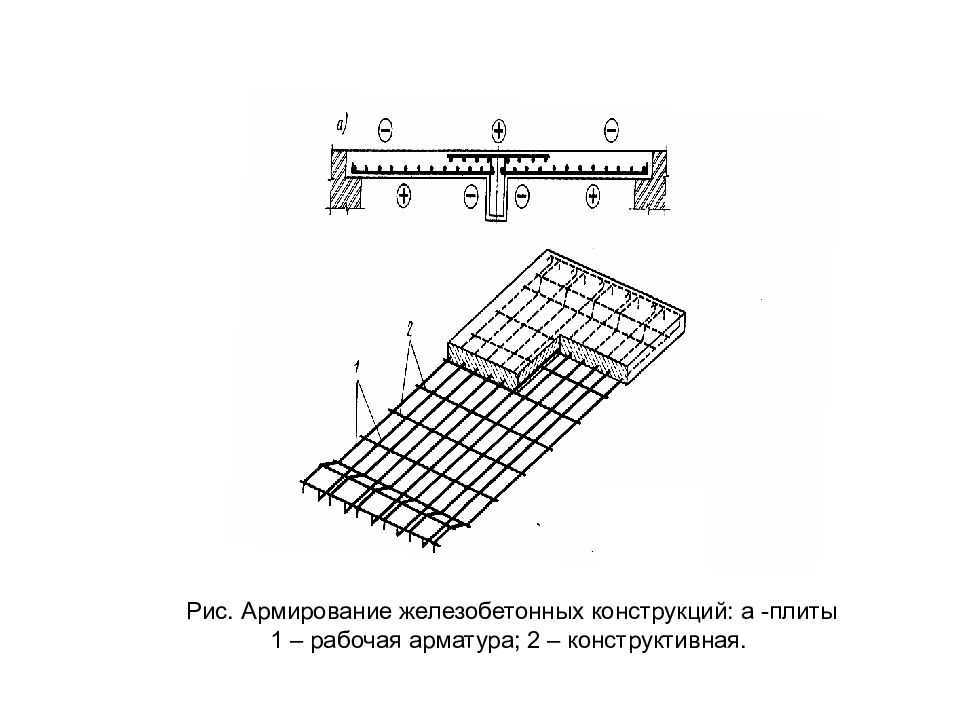
По назначению в бетоне арматуру разделяют на рабочую, распределительную, монтажную и хомуты.

Рабочая арматура воспринимает на себя главным образом растягивающие усилия, возникающие в железобетонных конструкциях от собственного веса и внешних нагрузок.

Распределительная арматура служит для равномерного распределения нагрузок между рабочими стержнями и для обеспечения совместной работы всех стержней арматуры. Кроме того, распределительная арматура связывает рабочие стержни между собой, препятствуя смещению рабочей арматуры при бетонировании.

Распределительная арматура соединяется с рабочей сваркой или проволочной скруткой, в результате чего образуется сетка или каркас.

Хомуты служат для предохранения от появления косых трещин в балке около опор и для связывания арматуры в каркас.

Монтажная арматура никаких усилий не воспринимает и служит как для сборки каркаса, так и для обеспечения во время бетонирования точного положения рабочей арматуры и хомутов. При бетонировании монтажная арматура иногда вынимается.

Рис. 42. Типы крюков на концах гладких арматурных стержней: 1 — полукруглый крюк прп машинном гнутье: 2 — полукруглый крюк с прямым участком прн ручном гнутье

Для лучшего закрепления арматуры в бетоне концы арматурных стержней, работающих на растяжение, делают загнутыми в виде крюков (рис. 42).

Арматура периодического профиля (см. главу VI), благодаря надежной анкеровке и повышенному сцеплению с бетоном, позволяет отказаться от крюков, что способствует экономии металла.

Для совместной работы арматуры с бетоном необходимо, помимо устройства крюков, оставлять вокруг каждого стержня слой бетона; для этого расстояние в свету между отдельными рядами арматурных стержней делается не меньше 25 мм, как показано на рис. 43. На этом же рисунке показан так называемый защитный слой бетона (между арматурными стержнями и поверхностью конструкции), предохраняющий арматуру от воздействия огня при пожаре и от ржавления.

Рис. 43. Расстояние между стержнями арматуры и величина защитного слоя бетона в железобетонной балке и плите (размеры в мм): а — армированной обычной арматурой: 1 — монтажные стержни; 2 — рабочие стержни плиты; 3 — распределительные стержни плиты; 4—рабочие стержни балки; б — армированной сварными сетками и каркасами: 1 — каркасы балки; 2 — сетки плиты

В соответствии с техническими условиями толщина защитного слоя для рабочей арматуры конструкций из тяжелого бетона должна быть:

При диаметре продольной арматуры более 35 мм рекомендуется толщина защитного слоя не менее 30 мм, а при применении фасонных прокатных профилей — 50 мм.

Хомуты и поперечные стержни должны отстоять от поверхности бетона не меньше чем на 15 мм. В железобетонных трубах расстояние от стержня продольной арматуры до внутренней поверхности трубы должно быть не меньше, чем до наружной.

В сборных железобетонных конструкциях заводского изготовления из тяжелого бетона марки не менее 200 толщина защитного слоя может быть уменьшена на 5 мм, но в любом случае должна быть не меньше 10 мм для плит и 20 мм для балок и колонн.

Распределительный фитинг | BPI Consulting

Сентябрь 2016 г.

(Примечание: все предыдущие публикации в категории базовой статистики перечислены справа. Выберите «Вернуться к категориям», чтобы перейти на страницу со всеми публикациями, отсортированными по категориям. Выберите эту ссылку для получения информации о программном обеспечении SPC для Excel.

В рамках процесса PPAP вы должны предоставить клиенту анализ возможностей процесса для только что выполненного пробного производственного цикла. Гистограмма собранных вами данных не выглядит нормально распределенной. График нормальной вероятности подтверждает ваши опасения — вы имеете дело с ненормальными данными. Вы запускаете преобразование Бокса-Кокса, чтобы увидеть, можно ли преобразовать данные в нормальное распределение. Трансформация не работает. Что теперь делать?

Для анализа возможностей процесса требуется нормальное распределение, чтобы можно было вычислить значение Cpk. Вы не сможете использовать Cpk. Вам придется провести нестандартный анализ возможностей процесса. Но чтобы выполнить этот анализ, вы должны определить, какое распределение лучше всего соответствует вашим данным.

В этой публикации объясняется, как выполняется подгонка распределения на примере экспоненциального распределения. Публикация в следующем месяце расширит это, чтобы сравнить несколько дистрибутивов, чтобы увидеть, какой дистрибутив лучше всего соответствует вашим данным.

В этом выпуске:

• Что такое распределительный фитинг?
• Не все соответствует нормальному распределению
• Определение лучшего дистрибутива
• Параметры распределения
• Оценка параметра
• Пример
• Подходит ли он?
• Резюме
• Быстрые ссылки

Пожалуйста, не стесняйтесь оставлять комментарии в конце этой публикации. Вы также можете скачать pdf-копию этой публикации по этой ссылке.

Что такое распределительный фитинг?

Подгонка распределения — это процесс, используемый для выбора статистического распределения, которое наилучшим образом соответствует данным. Примеры статистических распределений включают нормальное, гамма-распределение, распределение Вейбулла и распределение наименьших экстремальных значений.

В приведенном выше примере вы пытаетесь определить возможности вашего ненормального процесса. Это означает, что вы должны быть в состоянии определить, какое распределение лучше всего соответствует данным, чтобы вы могли определить вероятность того, что ваш процесс произведет материал, выходящий за рамки спецификаций. Важно иметь распределение, которое точно отражает ваши данные. Если вы выберете неправильное распределение, ваши расчеты будут неверными.

Коротко о самих данных. Данные должны быть непротиворечивыми и предсказуемыми, т. е. они должны быть получены в результате процесса, находящегося под статистическим контролем. Если процесс не находится под статистическим контролем, подгонка распределения не будет точной.

Не все соответствует нормальному распределению

Жизнь была бы прекрасна, если бы мы могли просто предположить, что наши данные имеют нормальное распределение. Это наиболее часто используемый дистрибутив. Почему? Потому что многие вещи нормально распределены. Но не все. Нормальное распределение определяется средним значением и стандартным отклонением. Он симметричен относительно среднего.

Распределения с асимметрией влево или вправо нельзя моделировать как нормальное распределение. Другие распределения ограничены и не могут быть смоделированы как нормальные распределения. И есть симметричные распределения, которые могут соответствовать вашим данным лучше, чем нормальное распределение.

Выбор неправильного распределения приводит к неточным результатам. Наша предыдущая публикация о ненормальных возможностях процесса дает пример того, как ваши расчеты возможностей процесса для Cpk неверны, если нет нормального распределения.

Определение наилучшего распределения

Несколько распределений обычно проверяются на данных, чтобы определить, какое из них лучше всего соответствует данным. Вы не можете просто посмотреть на форму распределения и предположить, что она хорошо соответствует вашим данным.

Как определить наилучшее распределение? Статистические методы используются для оценки параметров различных распределений. После завершения этой оценки вы используете методы оценки соответствия, чтобы определить, какое распределение лучше всего соответствует вашим данным. Существуют также визуальные методы, которые помогут вам решить, какой дистрибутив лучше всего. Сюда входит изучение гистограммы с наложенным распределением и сравнение эмпирической модели с теоретической моделью. Ниже эти методы рассматриваются более подробно.

Параметры распределения

Параметры распределения определяют распределение. Есть четыре параметра, которые в основном используются при настройке распределения. Вот эти четыре параметра:

• Местоположение
• Весы
• Форма
• Порог

Не все параметры существуют для каждого распределения. Например, нормальное распределение имеет только два параметра: местоположение (среднее) и масштаб (стандартное отклонение). Эти два параметра полностью определяют нормальное распределение. Подгонка распределения включает в себя оценку параметров, определяющих различные распределения. Четыре параметра более подробно определены ниже.

Параметр местоположения распределения указывает, где находится распределение по оси x (горизонтальной оси). На рис. 1 показаны два нормальных распределения. Значения местоположения разные. Синее распределение имеет положение 5. Оранжевое распределение имеет положение 10. Оба имеют одинаковое стандартное отклонение (или шкалу в терминах параметров).

Рисунок 1: Нормальное распределение с различными местоположениями

Масштабный параметр распределения определяет степень разброса в распределении. Чем больше параметр масштаба, тем больше разброс в распределении. Чем меньше параметр масштаба, тем меньше разброс в распределении. На рис. 2 показано логистическое распределение с тремя различными параметрами шкалы: 2, 5 и 8. Положение всех трех кривых — 0,9.0005

Рисунок 2: Логистическое распределение с различными параметрами масштаба

Параметр формы распределения позволяет распределению принимать различные формы. Два приведенных выше распределения, нормальное и логистическое, не имеют параметра формы. Форма определяется расположением и масштабом этих двух распределений. Другие распределения имеют параметры формы. Чем больше параметр формы, тем больше отклонение распределения влево. Чем меньше параметр формы, тем больше отклонение распределения вправо. На рис. 3 показано, как изменение параметра формы влияет на гамма-распределение. Параметр масштаба для гамма-распределения на рисунке 3 равен 2. Гамма-распределение не имеет параметра местоположения.

Рисунок 3: Гамма-распределение с различными параметрами формы

Пороговый параметр распределения определяет минимальное значение распределения по оси x. Распределение не может иметь значений ниже этого порога. На рисунке 4 показано гамма-распределение с тремя различными пороговыми значениями: 3, 6 и 9. Параметр масштаба и формы равен 2.

Рисунок 4. Гамма-распределение с различными пороговыми значениями

Оценка параметров

Для оценки параметров распределения можно использовать ряд статистических методов. SPC для Excel использует метод оценки максимального правдоподобия (MLE). В качестве примера мы будем использовать экспоненциальное распределение.

Экспоненциальное распределение является широко используемым распределением в проектировании надежности и используется для моделирования времени между отказами, когда блоки имеют постоянную частоту отказов. Это распределение имеет один параметр, и существует аналитическое решение для нахождения этого параметра. Предположим, у нас есть выборка размера n из одного распределения. Мы хотим знать, получена ли выборка из экспоненциального распределения.

Вы начинаете с функции плотности вероятности (PDF) для распределения. Экспоненциальная PDF определяется как:

, где b — параметр шкалы; b должно быть больше 0. Наша цель – найти значение b на основе наших выборочных данных. Каждый x _i имеет один и тот же PDF-файл, поскольку образцы взяты из одного и того же дистрибутива.

Функция правдоподобия случайной выборки L определяется как произведение каждого отдельного PDF:

Замена в экспоненциальном PDF дает:

Мы хотим найти значение b, которое максимизирует эту функцию правдоподобия. Вот хитрость с MLE. Легче свести к минимуму отрицательную логарифмическую вероятность. Взятие отрицательного логарифма обеих частей приведенного выше уравнения преобразует произведение PDF в сумму PDF.

Мы хотим найти значение b, которое минимизирует эту функцию. Чтобы найти это, вы берете частную производную от -ln L по b и устанавливаете это уравнение равным 0,9.0005

Решение для b дает следующее:

Это просто уравнение для среднего. Для экспоненциального распределения параметр масштаба, равный среднему значению, минимизирует логарифмическую функцию правдоподобия.

Это подход MLE. Расчеты становятся более сложными для большинства других распределений. Функция логарифмического правдоподобия должна быть дифференцирована по каждому оцениваемому параметру, при этом каждое из результирующих уравнений должно быть установлено равным нулю. Затем уравнения должны быть решены одновременно, чтобы найти параметры распределения. Численные методы должны использоваться для большинства распределений.

Пример

Предположим, у нас есть выборка из 100 точек данных. Скачать использованные данные можно по этой ссылке. Гистограмма (рис. 5) из 100 точек данных показывает, что данные не имеют нормального распределения.

Рисунок 5: Гистограмма выборочных данных

Обычно несколько распределений проверяются, чтобы определить, какое из них лучше всего соответствует данным. Для этой публикации мы просто будем использовать экспоненциальное распределение. Мы уже показали, что минимум логарифмической функции правдоподобия для экспоненциального распределения имеет место, когда параметр масштаба b равен среднему значению.

Среднее значение набора данных равно 2,975. Таким образом, экспоненциальная PDF становится:

Мы определили экспоненциальное распределение на основе наших данных. Но насколько хорошо это соответствует данным?

Подходит ли он?

Из вышеизложенного мы знаем, что когда параметр масштаба равен среднему значению, логарифмическая функция правдоподобия минимизируется, и это лучше всего соответствует экспоненциальному распределению. Но годится ли это?

Существует несколько способов оценки соответствия. Очень распространенный способ — вычислить статистику Андерсона-Дарлинга и определить p-значение, связанное с этой статистикой. Тест предполагает, что данные соответствуют указанному распределению. Низкое значение p означает, что предположение неверно и данные не соответствуют распределению. Высокое значение р означает, что предположение верно и данные соответствуют распределению.

В более ранней публикации было описано, как рассчитать статистику Андерсона-Дарлинга для нормального распределения. Процесс такой же для других распределений, за исключением того, что вы используете кумулятивную функцию распределения (CDF) для этого распределения в расчетах. Данные были проанализированы с использованием программного обеспечения SPC для Excel, и для экспоненциального распределения были получены следующие результаты:

• Статистика Андерсона-Дарлинга = 6,374
• p-значение < 0,001

Поскольку p-значение очень мало, вы делаете вывод, что экспоненциальное распределение не соответствует данным.

Есть также визуальные методы, которые можно использовать, чтобы определить, насколько хорошо они подходят. Один из них — наложение PDF-файла распределения на гистограмму данных. Это показано на рисунке 6.

Рисунок 6: Гистограмма с экспоненциальным pdf0002 Другой визуальный способ увидеть, соответствуют ли данные распределению, — это построить график PP (вероятность-вероятность). P-P отображает эмпирические значения CDF (на основе данных) в сравнении с теоретическими значениями CDF (на основе указанного распределения). CDF для экспоненциального распределения определяется как:

Если график PP близок к прямой линии, то указанное распределение соответствует данным. На рис. 7 показан график PP для данных в зависимости от экспоненциального распределения.

Рисунок 7: График PP для экспоненциального распределения

Данные на рисунке 7 не ложатся на прямую линию — еще одно свидетельство того, что экспоненциальное распределение не соответствует данным.

Краткий обзор

В данной публикации представлена ​​распределительная арматура. Распределения определяются параметрами. Были введены различные параметры (местоположение, масштаб, форма и порог). Метод оценки максимального правдоподобия используется для оценки параметров распределения по набору данных. В качестве примера использовалось экспоненциальное распределение. Также были введены методы проверки того, насколько «хорошо» распределение соответствует данным. Эти методы согласия включают статистику Андерсона-Дарлинга, сравнение гистограммы с функцией плотности вероятности и построение графика PP для сравнения теоретической кумулятивной функции плотности с эмпирической кумулятивной функцией плотности. В нашей следующей публикации мы рассмотрим, как сравнивать несколько распределений при попытке найти распределение, которое лучше всего соответствует данным.

Быстрые ссылки

Программное обеспечение SPC для Excel

Посетите нашу домашнюю страницу

Обучение SPC

Консультации SPC

Информация для заказа

Большое спасибо за то, что прочитали нашу публикацию. Мы надеемся, что вы найдете его информативным и полезным. Удачных графиков, и пусть данные всегда поддерживают вашу позицию.

С уважением,

Доктор Билл МакНиз
BPI Consulting, LLC

Свяжитесь с нами

Подгонка распределения – Учебное пособие

Вернуться к Учебнику

Подгонка распределения вероятностей или просто подгонка распределения – это подгонка распределения вероятностей к ряду данных, касающихся повторяющихся измерений переменного явления. Цель подгонки распределения состоит в том, чтобы предсказать вероятность или предсказать частоту появления величины явления в определенном интервале.

Подгонка распределения — это процедура выбора статистического распределения, которое наилучшим образом соответствует набору данных, сгенерированному некоторым случайным процессом. Другими словами, если есть какие-то случайные данные, и кто-то хотел бы знать, какое конкретное распределение можно использовать для описания данных, то ищется подгонка распределения.

Другим распространенным применением, в котором полезны процедуры подбора распределения, является проверка предположения о нормальности перед использованием какого-либо параметрического теста.

Отбор

результаты и выберите наиболее подходящую модель. Подходящие распределения «кандидатов» следует выбирать в зависимости от характера ваших вероятностных данных. Например, если кому-то нужно проанализировать время наработки на отказ технических устройств, ему следует подогнать неотрицательные распределения, такие как экспоненциальное или Вейбулла, так как время отказа не может быть отрицательным.

Выбор подходящего распределения зависит от наличия или отсутствия симметрии набора данных относительно среднего значения.

• Симметричные распределения. Когда данные симметрично распределены относительно среднего значения, а частота появления данных, удаленных от среднего, уменьшается, можно, например, выбрать нормальное распределение, логистическое распределение или t-распределение Стьюдента. .
• Распределение с перекосом вправо — когда большие значения имеют тенденцию быть дальше от среднего, чем меньшие значения, имеет место скошенное распределение вправо (т. е. имеется положительная асимметрия).
• Распределение с перекосом влево — когда меньшие значения имеют тенденцию быть дальше от среднего, чем большие значения, имеет место скошенное распределение влево (т. е. имеет место отрицательная асимметрия).

Методы подбора

Существуют следующие методы подбора распределения

• Параметрические методы, с помощью которых параметры распределения рассчитываются из ряда данных. Параметрические методы – метод моментов, метод L-моментов и метод максимального правдоподобия 9.0020
• Метод регрессии, использующий преобразование кумулятивной функции распределения таким образом, чтобы найти линейную зависимость между кумулятивной вероятностью и значениями данных, которые также могут нуждаться в преобразовании в зависимости от выбранного распределения вероятностей.

Критерии согласия

Критерий хи-квадрат используется для проверки того, поступила ли выборка данных из совокупности с определенным распределением. Другой способ взглянуть на это — спросить, соответствует ли частотное распределение определенному образцу.

Предположения – Данные получены из случайной выборки. Ожидаемая частота каждой категории должна быть не менее 5. Это восходит к требованию нормального распределения данных. Вы моделируете полиномиальный эксперимент (используя дискретное распределение) с критерием согласия (и непрерывным распределением), и если каждая ожидаемая частота не менее пяти, то вы можете использовать нормальное распределение для аппроксимации.

Certified Inventory and Warehouse Analytics Professional

Вернуться к учебнику

Получите признанный отраслевой сертификат – свяжитесь с нами

Пожалуйста, включите JavaScript в вашем браузере, чтобы заполнить эту форму.